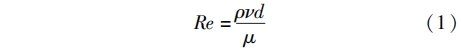摘要:超臨界二氧化碳循環發電技術采用超臨界狀態下的二氧化碳代替傳統水蒸氣工質,由于物性發生巨大變化,質量流量測量與計算方法需重新構建。本文開展了孔板流量計數值模擬研究,使用fluent軟件模擬計算了孔板直徑比、節流孔厚度、孔板厚度等結構參數對流量系數的影響,結果表明現行標準對超臨界二氧化碳并不適用。本文提出了針對超臨界二氧化碳工質的孔板流量計結構參數推薦范圍,在該范圍內絕大多數計算結果相對誤差小于2%,并針對入口邊緣鈍化提出了新修正系數,修正后計算結果相對誤差為0.11%~1.85%,滿足測量精度要求。
伴隨著經濟社會的不斷發展,我國發電機組在發電效率、能源結構、環境效益等多方面都面臨著轉型升級的嚴峻挑戰。中國在2007年已經成為全球溫室氣體第一大排放國家川。習近平總書記在聯合國-般性辯論會.上承諾[2],中國碳排放量力爭分別于2030年和2060年前實現達峰和中和,作為一種變革性火力發電技術超臨界二氧化碳循環是實現能源結構轉型進程中的重要手段。
隨著“雙碳”目標的逐步落實,超臨界二氧化碳(溫度高于303.98K、壓力高于7.38MPa)被廣泛應用,其作為工質的布雷頓循環具有極高的熱源適用性,可應用于太陽能、核能、余熱等多種場景。且由于超臨界二氧化碳密度大、黏性小、壓縮性好、循環過程無相變,相比于傳統水工質,超臨界二氧化碳循環珂以實現更高的循環效率,Dostal等[3]指出在透平人口工質溫度高于550℃條件下,超臨界二氧化碳循環發電系統性能顯著高于水循環系統。此外,配合間歇性、隨機性強的可再生能源供電以保障社會用電穩定是未來火力發電重要任務,超臨界二氧化碳系統靈活性高、能實現完全熱電解耦的特點也使其更能滿足未來火力發電的深度調峰需求。
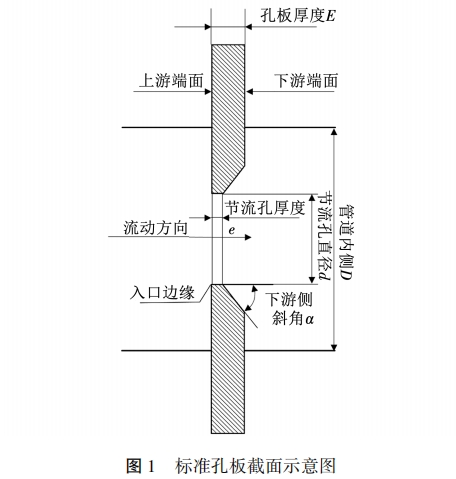
系統內部流動工質流量的正確測量是其得以應用的基礎。當前超臨界二氧化碳主要用于藥物/化學試劑萃取、油田驅油等溫度、壓力相對較低的場景,而超臨界二氧化碳循環系統需要二氧化碳工質達到極高的溫度與壓力,二氧化碳的密度、比熱、黏度等物性參數發生了顯著變化,對于該條件下二氧化碳流量測量,傳統流量測量方法將不再適用。孔板流量計是--種技術成熟且適合于高溫高壓流體流量測:量的方法,經過多年發展孔板流量計已形成標準化形式,主要包括兩部分,分別是具有直角邊緣的-段節流孔,以及在節流孔后具有一斜角的錐形擴流段,其結構如圖1所示。然而有關測量超臨界二氧化碳循環中工質流量的孔板流量計設計方案,國內外并無經驗借鑒。因此需要針對超臨界二氧化碳工質的全新特性,探究孔板結構參數的變化對于流量系數的影響,同時驗證現有標準中的相關規定對于超臨界二氧化碳工質是否適用。.
我國學者采用數值模擬為主,實驗驗證為輔的研究方式,以水或天然氣為研究對象,開展了管徑、孔徑厚度等結構參數對孔板流量計的影響研究。孔板直徑比、厚度等參數會顯著影響孔板的節流特性,從而影響流量計的計量性能。當直徑比小于0.3時,流量系數隨直徑比增加而快速下降,當直徑比大于0.3時,流量系數逐漸遞增,但增速較緩;直徑比在0.2~0.8范圍內時,流量系數隨β增大呈先減小后增大的趨勢,并以0.55為分界點,其中β在0.45~0.65之間時可控制誤差在3%以內。與直徑比不同,流量系數隨孔板厚度的變化特性較--致。厚度e增加,流出系數直線上升;林棋等人[4-5]也認為流出系數隨縮徑孔厚度增大而增大;在模型中考慮了引壓管的存在,結果顯示,e變化0.15mm時,流出系數變化1.56%;e變化1mm時,流出系數變化2.125%。
近年來的理論知識、不斷優化的算法以及不斷更新擴充的實驗數據庫等都保證了數值模擬研究的正確率與精度,因而逐漸成為主流研究方法之一。孔板流量計管道內部介質流動復雜,參數變化劇烈,采用數值模擬方法可以有效捕捉到管道內部的細微變化,因此是孔板流量計研究的有力工具。部分學者利用數值模擬對孔板流量計結構進行了優化設計。利用Fluent模擬了一種半雙曲線型的新式孔板流量計,并同時利用牛頓流體和非牛頓流體進行驗證,發現這種流量計可使內部介質近似無剪切流動,大大消除了渦流和停滯區等流動結構;研究發現在孔板流量計下游插入-個環可以有效減少壓力損失,并利用數值模擬和遺傳算法優化結構,可減少33.5%的壓力損失,極大的降低了能耗和成本。
因此,本文進行了孔板流量計結構參數對于流量系數影響的模擬研究,包括直徑比、節流孔厚度、孔板厚度等結構參數,明確了在超臨界二氧化碳工質典型工況下不同結構參數對流量系數的影響,同時將通過現行孔板流量計國際標準文件中經驗公式計算得到的結果與數值模擬結果進行比較,提出了針對超臨界二氧化碳工質的孔板流量計結構參數推薦范圍與推薦設計值,提升了其測量精度。除此之外,還探究了孔板人口直角邊緣鈍化對孔板流量計測量精度的影響,并據此提出了新的針對現行孔板流量計國際標準文件中經驗公式計算得到的流量系數的修正系數。
1.計算模型與模擬方法
1.1模型建立與網格劃分
根據標準文件[1]規定的孔板流量計結構設計與參數要求,本文分別建立了DN25和DN200兩種管徑的孔板流量計,結構參數如表1所示,在后文進行相關研究時均以該表中的結構參數為基礎參數,依據該參數使用SolidWorks軟件建立了孔板流量計及其前后一定長度管道的幾何模型,如圖2所示。


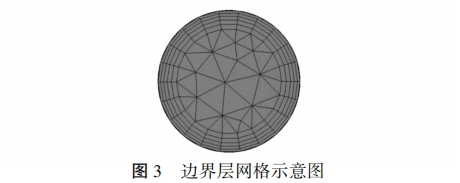
本文采用非結構化網格進行模擬計算,利用AnsysMeshing軟件將孔板流量計管道劃分為四面體網格和六面體網格相結合的混合形式。除此之外,為了準確捕捉到流場內的細微變化,在介質與管道內壁接觸處進行邊界層的網格劃分,采用平滑過渡法,第一層高度根據面網格和過渡比進行確定,最大層數為5層,增長率為1.2,這時邊界層總厚度是變化的,對于復雜流動更有效,結果如圖3所示。
為提高節流孔板內部及其到前后取壓截面處的模擬精度,利用影響球對孔板前后長度為D的流場范圍內進行了局部網格加密,網格數量過少會導致計算精度不足,而過多的網格數量則會無謂地加大計算工作量,降低計算速度。本文對DN25和DN200兩種管徑不同的管道進行網格數量與計算結果無關性的驗證,綜合計算精度與計算速度考慮,對于DN25管道,選取網格數分別為956036和1190483時,在各點測出的壓力相差均小于0.01%,因此選擇劃分網格數為956036;對于DN200管道,選取網格數分別為2308874與4328293時,在各點測出的壓力相差均小于0.01%,因此選擇劃分網格數為2308874。
1.2模擬程序參數設置
1.2.1物性參數設置
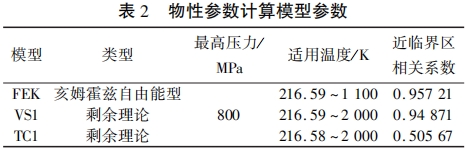
Refprop軟件由NIST開發,該軟件含有豐富的數據庫以及適用于超臨界CO,的多個狀態方程。本文通過在Fluent軟件中激活NISTRealGas模型[川進行調用,計算超臨界二氧化碳流體的物性參數。其中物性參數采用FEK狀態方程模型計算,黏度采用VS1模型,導熱系數采用TC1模型,各模型的相關參數如表2所示。
1.2.2邊界條件設置
本文針對超臨界二氧化碳鍋爐人口處的循環工質進行流量系數測量的數值模擬研究,設置了質量流量人口與壓力出口,溫度、壓力等參數的選取為超臨界二氧化碳鍋爐入口處工質典型參數,即750K、21MPa。由于循環系統運行于高壓環境,管道的壓力損失相較而言很小,因此可認為管道壓力為恒定.值,壓力出口參數設置與人口相同,其余參數保持默認不變;由于超臨界二氧化碳鍋爐人口處管道一般采取嚴格保溫措施,因此可忽略壁面與工質間的換熱,設置為絕熱邊界。
1.2.3數值模型設置
本文主要模擬超臨界二氧化碳工質流經孔板流量計的流動過程,基本方程包含質量、動量和能量輸運方程,由雷諾數的定義公式
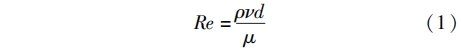
計算可知本文針對的超臨界二氧化碳工況下雷諾數均遠大于4000,因此管道內的流動均處于湍流狀態,在進行數值模擬時需進行湍流模型的設置,本文選擇SSTh-ɷ湍流模型。
1.2.4求解參數設置
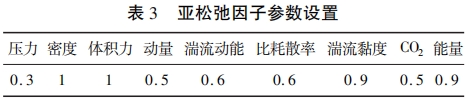
FLUENT中的亞松弛因子主要控制計算過程中每次迭代的變化量,可以通過減少兩層次之間計算.結果的差值從而促進收斂。本文設置的亞松弛因子如表3所示。
1.3模型的驗證
基于上述設置,本文針對溫度為535.1~642.5K、壓力為19MPa、質量流量為1.28kg/s的實驗工況進行了模擬研究,模擬的孔板結構參數、溫度、壓力、流量等參數以及數據處理方法均與實驗保持--致,得到了超臨界二氧化碳工質的流量系數。將模擬計算得到的流量系數與實流測量結果進行對比,結果如圖4所示。,通過數值模擬得到的流量系數與實驗數據總體趨勢相似,在數值上均高于實驗數據,但相對于實驗數據的偏差較小,偏差為1.62%~2.69%。
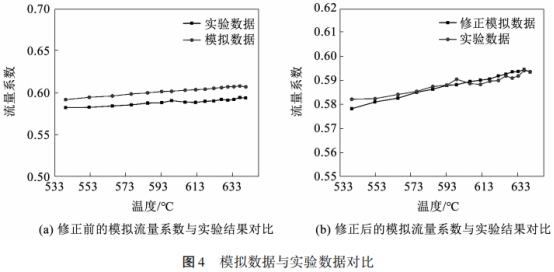
造成偏差的原因可能有多種,如實驗選用測量儀表具有一定的不確定度、模擬參數的設置無法與真實情況完全對應、收斂判據設置不嚴格等等。為了降低模擬結果與實驗數據的偏差,本文分別按各模擬結果相對同工況下實驗數據的偏差平均值進行修正。模擬得到流量系數相對實驗數據平均增大0.013,因此對模擬結果減去該修正值,修正后相對偏差為0.016%~0.674%。
上述結果說明數值模擬方法與實驗結果的一致性較好,因此本文建立的數值模擬方法可用于后續進一步的研究。
2孔板結構參數對流量系數影響
2.1直徑比的影響
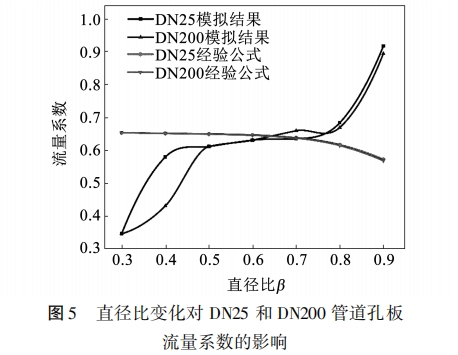
直徑比會顯著影響孔板對于介質流過的節流效果,改變介質流過的速度、壓力等參數,是影響孔板流量計測量性能的首要因素。ISO國際標準中規定,孔板流量計的直徑比一般在0.1~0.75內變化,本文分別選取直徑比在0.3~0.9之內的7個工況進行了模擬計算,探究孔板流量計直徑比對流量系數的影響,得到的結果如圖5所示。
對數據進行分析可知:
(1)孔板流量系數隨直徑比的變化趨勢與管徑無關。隨著孔板直徑比增大,DN25和DN200管道內孔板流量系數呈現近似相同變化趨勢;上升-平穩-.上升,主要區別在于前者在β為0.4~0.8范圍內較平穩、而后者在0.5~0.8范圍內較平穩;
(2)標準文件[10]中經驗計算公式的結果隨直徑比增加而逐漸下降,其中直徑比在0.3~0.6范圍內時下降趨勢較平緩,當超過0.6時下降值逐漸增大;
(3)孔板流量系數在β為0.3~0.6時小于經驗公式計算值,此范圍內使用經驗計算公式會使測量結果較真實值大2.45%~47.03%;β在0.7~0.9時孔板流量系數大于經驗公式計算值,此時使用經驗計算公式會使測量值比實際值小0.5%~60.19%;
(4)當直徑比在標準文件[10]規定的0.1~0.75范圍內時,孔板流量系數的模擬結果與經驗公式計算結果的相對誤差波動較大,如對DN25管道而言,β為0.3時相對偏差達到47.03%,而β為0.7時相對偏差僅為0.5%。因此對于超臨界二氧化碳工質而言,孔板直徑比的選擇范圍應較標準規定范圍縮小;對于超臨界二氧化碳工質而言,直徑比在0.6~0.7范圍內時孔板流量系數的模擬結果與經驗公式計算結果的相對誤差較小,其中DN25管道相對誤差為0.5%~2.45%,DN200管道相對誤差為2.27%~3.6%。
2.2節流孔厚度的影響
孔板節流孔厚度決定了超臨界二氧化碳工質流過收縮管道的長度,是影響孔板節流能力的主要參數之一,會對工質流過孔板的流速、壓力等參數產生影響,進而影響測量結果。標準文件[10]規定標準孔板節流孔厚度應在0.005D~0.02D之間,對應DN25管道的e應在0.115~0.46mm,DN200管道的e應在0.695~2.78,本文分別模擬了DN25管道e為0.1~0.7mm、DN200管道e為0.2~4.2mm時超臨界二氧化碳工質流過節流孔板的流量系數變化,為便于對比,以e/D為橫坐標將結果表示在圖6中。
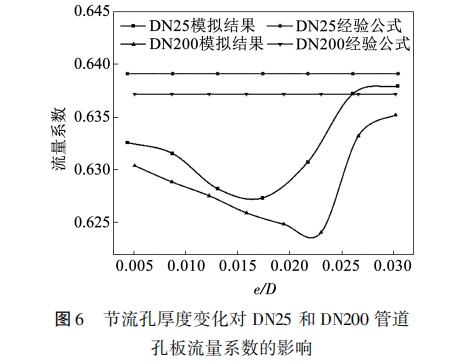
對數據進行分析可知:
(1)孔板流量系數隨e/D的變化趨勢與管徑無關。隨著e/D逐漸增加,DN25和DN200管道內孔板的流量系數均呈現先減小后增大的趨勢,分別在e/D為0.017和0.023時達到最小值,此后流量系數先急劇增大,隨后保持平緩增長;
(2)標準文件[I0]中經驗計算公式的結果不隨節流孔厚度而發生改變,其中DN25管道的經驗公式計算結果略大-一些,模擬得到的DN25和DN200管道的流量系數均小于經驗公式計算結果,其中前者的相對誤差為0.18%~1.84%,后者的相對誤差為0.31%~2.05%;
(3)在標準文件[10]規定孔板節流孔厚度范圍內,孔板流量系數模擬結果與經驗公式的相對誤差均在2%以下,因此標準中規定的孔板節流孔厚度范圍可以接受;同時還發現當節流孔厚度超過規定范圍一定值后,相對誤差仍可接受,甚至相對誤差還可能減少,如DN25管道的e為0.6mm、0.7mm時,均超出了規定上限0.46mm,但相對誤差分別達到了0.3%和0.18%,因此標準中規定的節流孔厚度范圍在針對超臨界二氧化碳工質時可以適當擴大,推薦DN25管道孔板節流孔厚度可在0.004D~0.03D內變化,DN200管道在0.005D~0.03D范圍內;
(4)基于模擬結果給出相對誤差更小時對應孔板節流孔厚度的推薦值,其中DN25管道孔板在e/D為0.004~0.008及0.02~0.03之間,即e為0.1~0.2mm.0.5~0.7mm時,相對誤差小于1.5%;DN200管道孔板在e/D為0.005~0.012及0.027~0.03時,對應e為0.7~1.7mm及3.7~4.2mm時,相對誤差小于等于1.5%。
2.3孔板厚度的影響
由圖1可知,標準孔板在節流孔之后還設置一定長度的錐形擴流段,與節流孔段共同組成孔板的節流段,該擴流段長度也會對孔板的節流能力產生影響,從而改變工質流過孔板后的速度、壓力等參數,對測量精度產生影響。標準文件[10]規定孔板厚度E應在e~0.05D之間,對應DN25管道的E應不大于1.15mm,DN200管道的E不超過6.95mm。
本文在保持節流孔厚度不變的情況下,分別設置了不同的孔板厚度用以探究流量系數的變化,其中DN25管道孔板厚度E為0.5~1.4mm,DN200管道孔板厚度E為3~8mm,模擬結果如圖7所示。
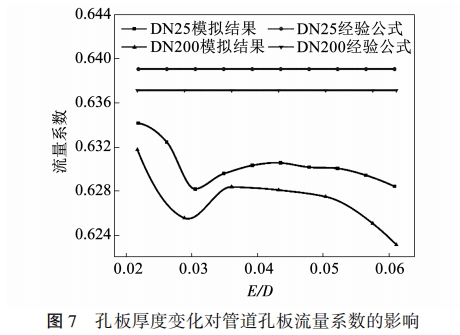
對數據進行分析可知:
(1)孔板流量系數隨E/D的變化趨勢與管徑無關。隨著E/D逐漸增加,DN25管道和DN200管道內孔板流量系數呈現近似相同的變化趨勢:即下降上升-平穩-下降,主要區別在于DN200管道內孔板流量系數下降和上升的趨勢更加明顯;
(2)流量系數經驗計算公式的結果不隨孔板厚.度而發生變化,其中DN25管道的經驗公式計算結果偏大--些,DN25和DN200管道的流量系數均小于經驗公式計算值,因此當使用經驗公式進行工質流量計算時會造成計算結果偏大;
(3)在標準文件[10]規定孔板厚度范圍內,DN25和DN200管道內孔板流量系數與經驗計算公式的相對誤差均在2%以下,因此標準中的規定范圍可以接受,但該規定范圍對于超臨界二氧化碳工質可適當擴充,如模擬結果所示,當DN25和DN200兩種管徑的孔板厚度E達到0.06D左右時,雖然已經超出了規定的0.05D這一限值,但相對誤差仍小于2%,處于可接受的范圍,但依據變化趨勢可以合理預測,當孔板厚度繼續增加時,相對誤差將大于2%,因此建議對于超臨界二氧化碳工質而言,孔板.厚度可設置在0.02D~0.06D之間。
2.4孔板流量計結構參數設計建議
通過對孔板流量計各結構參數的模擬研究,明確了在進行超臨界二氧化碳工質質量流量測量時,孔板流量系數隨各結構參數的變化趨勢與相對誤差,本節主要對以上模擬結果進行總結分析,參考《用能單位能源計量器具配備和管理通則》中的精度規定,,給出了針對超臨界二氧化碳工質的孔板流量計結構參數推薦設計范圍,在該范圍內經驗計算公式的計算結果可滿足2.5精度等級要求,還進一步提出了該范圍內精度相對更高的結構參數推薦值,將以上結果與現行國際標準ISO5167-2:2003中標準孔板流量計各結構參數的規定范圍進行對比,如表4所示。
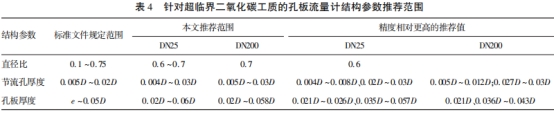
可以看出,對于超臨界二氧化碳工質而言,標準文件[10]規定的孔板流量計各結構參數的設計范圍并不完全適用,其中直徑比的規定范圍過大,對應的流量系數的相對誤差也波動較大,從0.5%到47.03%不等,而當直徑比在0.6~0.7范圍內時,可將相對誤差有效降低至0.5%~3.6%;在標準文件[10]規定的節流孔厚度、孔板厚度等參數范圍內,絕大多數流量系數的相對誤差可控制在2%以下,因此其規定范圍可以繼續使用,同時本文的數值模擬結果顯示,當孔板的以,上幾個結構參數的數值超.出其規定范圍時,最大相對誤差也僅為2%左右,因此對于超臨界二氧化碳工質而言,孔板的節流孔厚度、孔板厚度等參數均可一定程度上超出標準中的規定范圍,相對誤差也可接受。
3入口直角邊緣尖銳度及其修正系數的模擬研究
一般而言,孔板人口邊緣應該是尖銳的,其與超臨界二氧化碳工質首先直接接觸,如果其尖銳度不夠的話則無法保證對于工質的節流作用達到預期,因而會對測量精度產生影響。在孔板實際工作過程:中,可能存在加工精度不足、工質磨損、腐蝕等問題的存在,造成直角邊緣變鈍,故標準文件[10]規定,孔板人口邊緣的圓弧半徑應小于等于0.0004D,在此限值之內的誤差是可以接受的,若超過這一-限值,則無法保證測量精度,應進行相應的維修、更換或修正等。本文模擬了孔板人口邊緣圓弧半徑為0~0.015D時孔板的流量系數變化趨勢,結果如圖8所示。
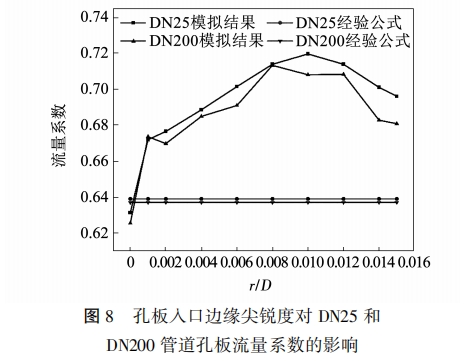
分析結果可以得出:
(1)孔板人口邊緣尖銳度對于孔板流量系數的影響趨勢與管徑無關。隨著孔板人口邊緣逐漸變鈍,DN25和DN200兩種管道的孔板流量系數呈現近似相同的變化趨勢,均隨著人口圓弧半徑的增大而先增大后減小,分別在r達到0.01D和0.008D時流量系數達到最大;
(2)孔板人口邊緣開始鈍化時,流量系數顯著增加,遠大于經驗計算公式結果,因此造成使用經驗計算公式時得到的工質質量流量相對真實值很小,其中DN25管道內相對誤差為5.16%~12.61%,DN200管道的相對誤差為5.13%~11.96%;
(3)對于超臨界二氧化碳工質而言,當孔板人口直角邊緣變鈍后,應立即進行相應的處理或流量系數的修正,否則誤差將會變得很大。
當使用標準文件[10]給出的不同邊緣尖銳度對應的修正系數b進行孔板流量系數的修正時,可以--定程度上減少流量系數的相對誤差。本文使用表5中的修正系數b對經驗公式計算結果進行修正,結果如圖9所示。

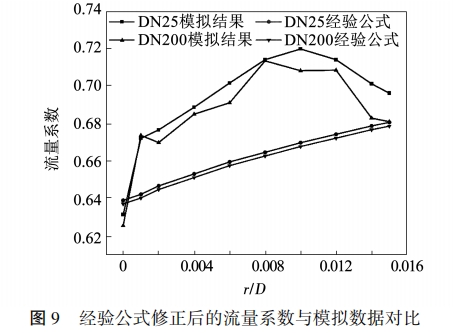
結果顯示,對于超臨界二氧化碳工質而言,當使用修正系數b進行孔板流量系數的修正后,僅可使部分邊緣圓弧半徑對應的孔板流量系數相對誤差降低到可以接受的程度,而大部分情況下相對誤差仍比較大,如DN25管道多數情況下的流量系數相對誤差在4.41%~6.94%之間,DN200管道的相對誤差多數在3.74%~7.11%,因此該修正系數b對于超臨界二氧化碳工質并不適用。
對DN25和DN200管道的模擬流量系數及經驗公式計算結果求平均,得到針對超臨界二氧化碳工質的不同孔板邊緣尖銳度對應的修正系數b,如表6所示。將更正的修正系數應用于模擬數據,結果如圖10所示。
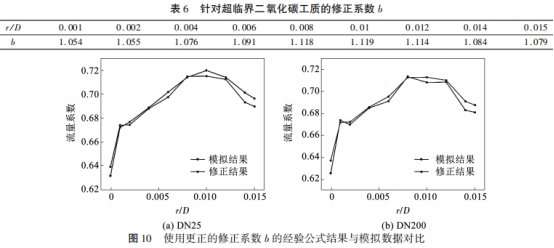
可以看出,當使用更正后的修正系數b進行孔板的流量系數經驗公式計算結果的修正后,得到的流量系數與模擬結果擬合較好,其中DN25管道相對誤差為0.11%~1.21%,DN200管道相對誤差為0.11%~1.85%。
4結論
本文開展了孔板流量計的數值模擬研究,探究了孔板的各結構參數對超臨:界二氧化磯工質流量系數的影響,基于此給出了孔板流量計結構參數的設計建議,并且探究了人口直角邊緣尖銳度對流量系數的影響,得到的主要結論如下:
(1)現行標準文件中的孔板流量計結構參數的規定范圍測量相對誤差在0.5%~47%的較大范圍內波動,對于超臨界二氧化碳工質并不適用。
(2)本文針對超臨界二氧化碳工質提出了孔板.流量計結構參數推薦設計范圍,其中直徑比應為0.6~0.7,節流孔厚度應為0.004~0.03倍的管道內徑,孔板厚度應為0.02~0.06倍的管道內徑,在該范圍內絕大多數工況下流量系數的相對誤差可控制在2%以下;
(3)孔板人口邊緣鈍化會使流量系數顯著增加,且修正系數b并不能使相對誤差降低至可以接受的范圍,修正后相對誤差仍有約3.74%-7.11%,本文針對不同工況提出不同修正參數,修正后經驗公式的相對誤差降低為0.11%~1.85%。
本文來源于網絡,如有侵權聯系即刪除!