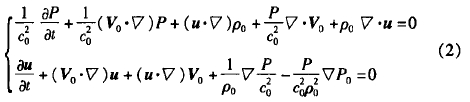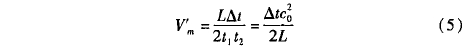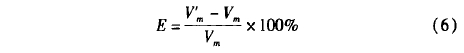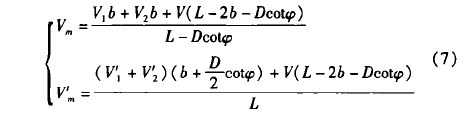摘要;超聲流量計測量過程探頭大小和結構設計所中探頭對流場的干擾是流量計流聲耦合仿真,定量分析了引起的執流效應、計算實檢量計探頭擾流的系統偏差;了聲道速度分布、探失聲壓1系統偏差。”i并利用分段加極平均的方式,這一少靠群進更長聲道長度情況下的探共挽流系統偏差。
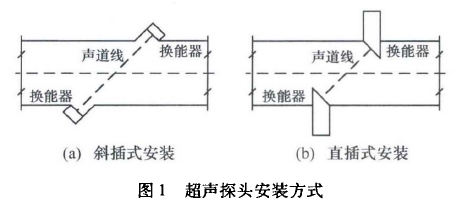
超聲流量計由于其無壓損、易安裝、精度高等優點,近年來得到了廣泛應用。超聲流量計是通過測量超聲波在流體中順流和逆流的時間差,計算聲道上的平均流速,再對不同聲道高度的平均流速進行積分,從而求得流量"。常見的探頭安裝方式如圖1所示,在探頭附近容易產生旋渦,影響了時差的測量。
利用CFD方法和實流.實驗研究了不同探頭插人深度時超聲流量測量的偏差。為了分析系統偏差的來源,Loland等利用PIV、LDV和CFD研究了探頭空腔內的局部流動結構;對探頭空腔內的流動也進行了細致的實驗研究。兩人的研究關注點在于流場,實際上流量計.測到的聲波信號里體現了波束范圍內流動的影響和壁面反射對聲波信號的干擾,流場和聲場兩者耦合作用共同造成了流量測量的偏差。
為了研究超聲流量計探頭擾流影響的機理,合理修正探頭擾流影響造成的系統偏差,利用多物理場仿真軟件對圖1(a)中的管道模型進行了流聲耦合仿真,分析了管道探頭模型中的流場細節和超聲波耦合傳播方式,并通過互相關算法計算時差,探討了探頭擾流和壁面反射作用對流量測量的影響。
1計算模型
仿真計算采用多物理場建模軟件COMSOL。首先進行流場仿真,計算模型為帶有--對超聲探頭安裝孔的管道,長度為300mm,直徑為70mm,探頭安裝孔直徑為14mm,按照45°聲道角分布于管道兩側,如圖2所示。流場仿真采用不可壓縮流動k-&湍流模型來模擬管道中流場的流動過程,并用PARDISO算法進行穩態求解,管道平均流速為3m/s。
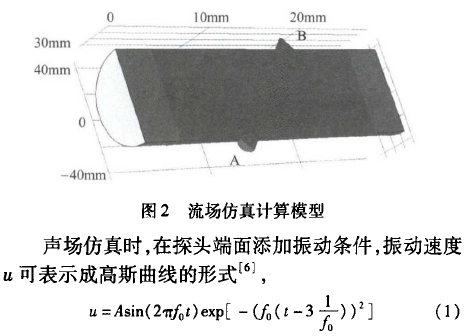
式中ƒ0為振動頻率,A為振動幅值。假設理想介質水域為連續介質,聲波在水域中的能量損耗為零,利用聲波在流體中的連續性方程,并通過MUMPS算法進行瞬態求解,對聲波在水流中傳播的方式進行仿真,
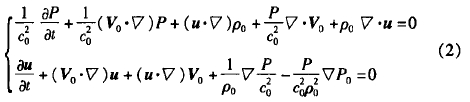
式中,P為聲壓;P0為流壓力;po為流密度;c0為聲速;V0為流速。本文中聲速C0設置為1481m/s。分別在探頭A探頭B端添加式(1)振動速度u,為減少計算量,設置了較低的振動頻率(0.2MHz)。
2仿真結果分析
2.1流場仿真結果
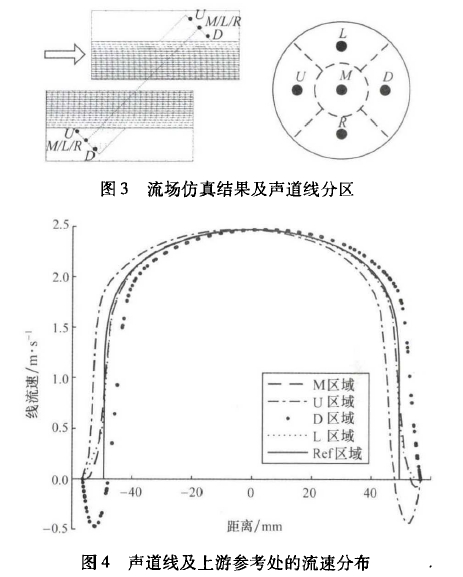
計算得到的探頭處流場如圖3所示,探頭附近存在旋渦。把探頭端面分別分為5個區域,以5個區域的中點M、U、D、L、R作為計算依據,分別提取5條連線上的流速分布,比較不同區域的流速變化,如圖4所示。各個點與中心M的距離為3.9mm。
圖4中橫坐標表示聲道方向探頭面與聲道中心的距離;縱坐標表示聲道方向的流速,A至B方向流速為正;R區域與L區域流速分布相同;Ref是指參考位置即未受到探頭擾流處,壁面連線之間的區域。探頭A的D區域和探頭B的U區域流場有明顯的速度變化,這是因為在探頭安裝孔處形成了旋渦,流速在這兩個區域內變化最為劇烈,而且相對流場而言,安裝孔內的旋渦方向和大小并不相同;M區域和L區域處的流場相類似,受旋渦影響較小。
2.2聲場仿真結果
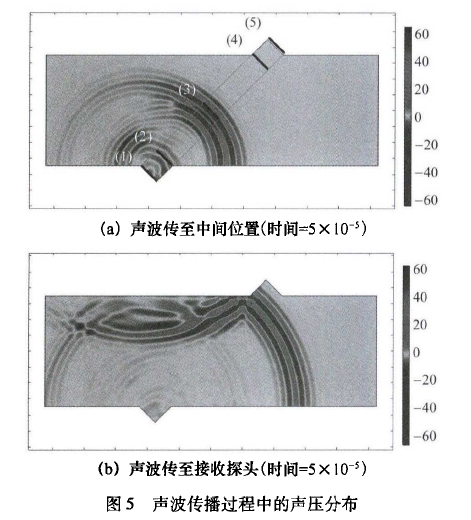
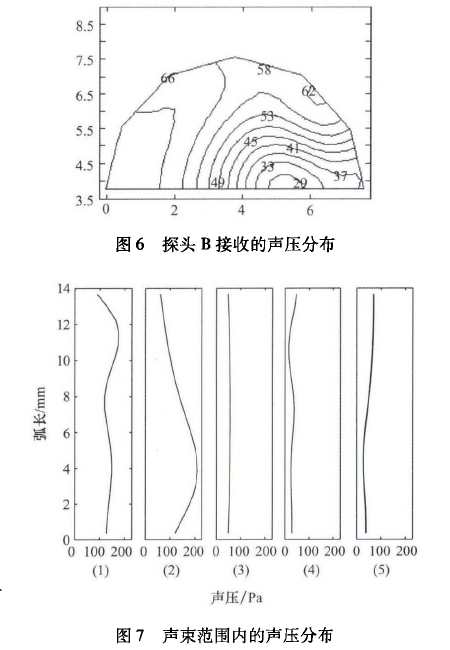
圖5展示了探頭A發射超聲波時,超聲波的傳播過程。在探頭A、探頭B的壁面處,超聲波發生了反射,反射信號和原信號相互疊加,造成了接收面聲壓的不對稱,進而影響傳播時間的測量。探頭B接收聲壓的分布情況如圖6所示,聲壓在接收面上非均勻分布,在接收面上分布-一個低壓區,低壓區中心位于中心偏下游的位置。
圖7為超聲傳播過程中不同位置聲壓振幅的分布情況,其中位置1~位置5已在圖5(a)中標注,統計的是聲波經過該位置的聲壓變化的振幅。在探頭A處的壁面反射造成了發射聲壓分布的畸變,在傳輸過程中逐漸減少了它的影響,所以探頭B所接收的聲壓主要受到B處壁面反射的影響,在探頭B附近低壓中心從上游逐漸向下游移動。
2.3傳播時間及流速計算
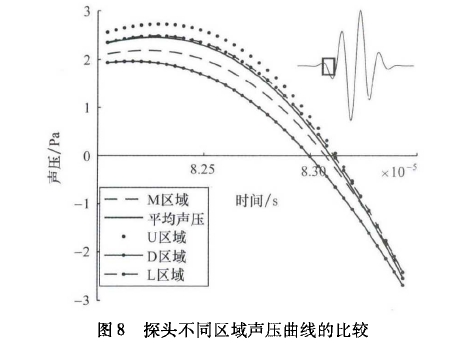
由于旋渦和璧面反射的影響,靠近探頭邊緣區域的聲壓曲線存在一定畸變。探頭B不同區域接收的聲壓與平均聲壓的關系如圖8所示。其中實線代表平均聲壓,虛線代表M區域處的聲壓變化。聲波傳播過程中,受到不同聲波傳播路徑和壁面反射的影響,接收面不同位置,接收聲壓幅值與過零點有明顯的區別。M區域處聲壓曲線幅值略高于平均聲壓曲線、過零點與平均聲壓曲線接近;U區域和D區域處聲壓曲線過零點與平均曲線有較大差異。
由于探頭不同區域聲壓變化曲線的差異,采用平均聲壓曲線來計算時間差,平均聲壓的計算結果接近聲壓中心,而且有更好的穩定性。探頭A、探頭B接收到的平均聲壓變化曲線如圖9所示,探頭A由于流體的減速作用收到波形略晚,兩個波形的相似度較高。利用互相關函數計算時差:
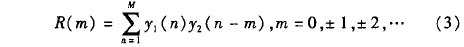
式中,y1(m)和y2(m)為探頭A、探頭B接收聲壓信號;m為數據長度,由互相關理論,當互相關函數取得最大值的時間位移,對應的是兩波形之間的時差。對R(m)進行優化求解,假設在m0點處取得最大值,可以求得時差△t:
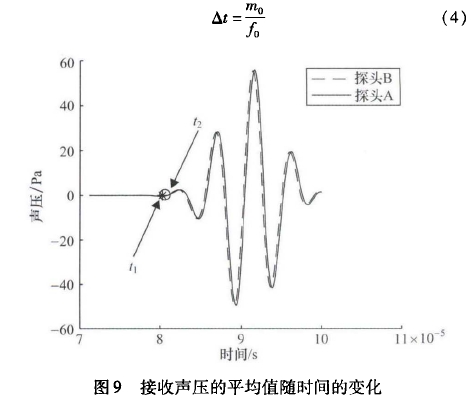
實際流量計測量時,通常是通過正逆向傳播時間T1、t2去和時差△t計算流速,由于流速遠小于聲速u0<<C0,可以進一步得到:
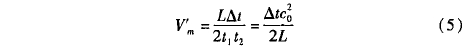
式中,L為聲道長度。將△t代人到式(5)中,可以解得聲道方向的平均流速V'm。聲場仿真計算中,△t=1.986x10-7s,L=113.0mm,求得V'm=I.928m/s。
對比管道流場計算結果,對聲束范圍內流速取平均值,求得V'm=1.934m/s,未受到探頭擾流區的聲道方向平均流速Vm=2.247m/s,求得聲場和流場計算的系統偏差E分別為一14.2%和-12.5%。兩者的差異體現了壁面反射對修正系數的影響。
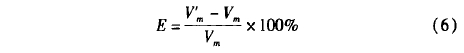
3推論和討論
超聲探頭對流場的擾動通常只發生在探頭附近--定范圍內,該范圍之外流場與上游充分發展的流場相同,因此可以用加權平均的方式將第2節中的計算結果向更長的聲道進行推論。在圖10所示的探頭安裝方式下,聲道角度為φ,探頭直徑為D。假設探頭在一定范圍內影響流場,上下游流場受影響的范圍為b,所以將流場沿聲道方向劃分成3個區域,分別為兩端的流場受影響速度區和中間的非影響速度區。
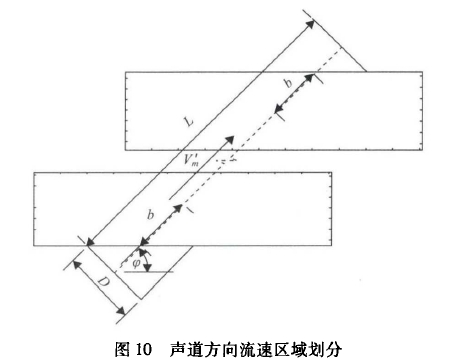
通過流場和聲場耦合仿真計算3個區域內平均投影速度,然后用加權分析的方法計算凸出效應造成的系統偏差,如式(7)所示。
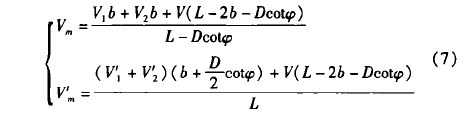
式中,V1、V2分別為未受到探頭擾流處上下游受影響速度區,聲道方向的平均流速;V'1、V'2分別為探頭擾流處,上下游受影響速度區,聲道方向的平均流速;V為非影響速度區,聲道方向的平均流速。其中幾何尺寸L、D、φ為固定值,V1、V2可以正確計算,所以確認b的范圍和V'1、V'2的值是確定修正系數的關鍵。
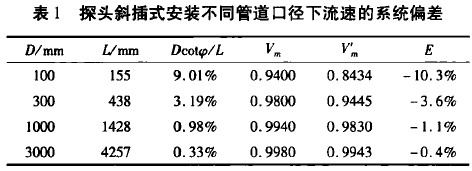
通過對圖4分析可知,在這種安裝方式下,在管道中心位置附近,各方向的流速是相近的,流速差值小于1%,可以認為管道中心附近為非影響速度區;在管道中心兩側,不同區域的流速變化情況不同,可以認為受影響速度區的范圍b=3.535D。通過耦合仿真計算,將非影響區域的流速平均值V=2.458m/s和平均聲壓計算流速值V"m=1.928m/s帶人式(7)中,求得上下游影響區域內的平均流速(V'1+V"2)/2為1.928m/s。再利用式(7)進行加權計算,可以推算出更長聲道時的探頭擾流影響,設定非影響區域的流速為1,求得不同管道口徑下,流速的系統偏差E如表1所示,其中聲道角度φ=45°,探頭直徑D=14mm。
4結論
超聲流量計探頭局部結構帶來的擾流效應造成了其流量測量的系統偏差,這一偏差通常利用實驗室實流校準來修正。為了更好地分析探頭擾流影響機理,利用多物理場仿真軟件對其進行了流聲耦合分析,主要結論如下:
①探頭凹坑內存在低速區且有漩渦,聲束范圍內各區域的平均流速與探頭中心區域上的平均流速不同,再加上探頭附近的壁面聲波反射,造成探頭端面不同區域接收到的聲壓信號有差異,流量計測到的聲波傳播時間體現的是聲壓信號統計平均的結果。
②對于帶有直徑14mm的斜插縮進式探頭的DN70流量計,按照探頭收到的面平均聲壓信號計算時差,探頭擾流造成的系統偏差約為-14.2%。
③在仿真結果的基礎上,假設探頭擾流影響范圍只限于其附近一定范圍,利用分段加權平均的方式,推導了更長的聲道長度情況下的探頭擾流系統偏差,發現該偏差均為負偏差,其絕對值近似等于探頭縮進比,隨著聲道長度的增加而降低。
本文來源于網絡,如有侵權聯系即刪除!