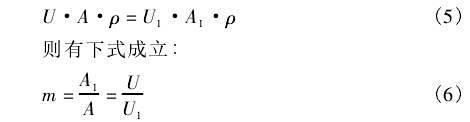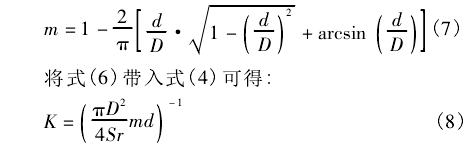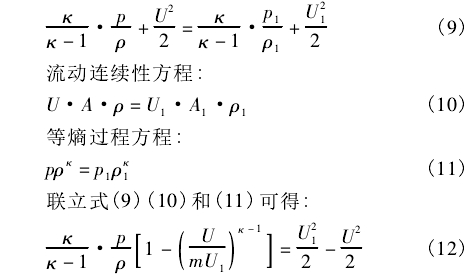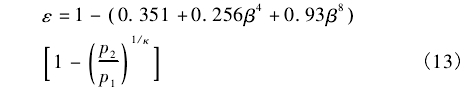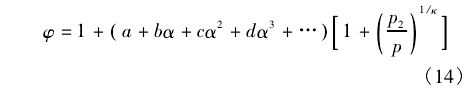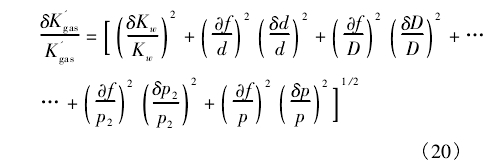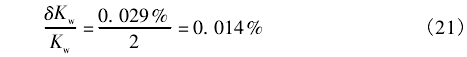摘要:基于渦街流量計基本原理,結合流體力學分析了介質可壓縮性對渦街流量計計量特性的影響。考慮到渦街流量計流動截面突然改變導致流體介質參數發生改變的現象與差壓式流量計有相似之處,類比標準孔板的介質可膨脹性系數經驗公式提出基于介質可壓縮性的渦街流量計儀表系數修正數學模型。通過最小二乘擬合對實流標定實驗數據進行數值分析得到儀表系數的可壓縮性修正公式。最后分析了修正儀表系數的誤差和不確定度,最大誤差為-0.64%,相對擴展不確定度均在1%以內。研究結果對采用蒸汽介質的渦街流量計儀表系數跨介質標定具有指導意義。
0引言
近年來渦街流量計依靠其結構簡單、無可動部件、壓損小、量程比寬等優點被廣泛應用于液體、氣體和蒸汽等介質的流量計量領域中。目前,國內外對于渦街流量計的量值溯源,普遍認為可以進行跨介質標定”在一定雷諾數范圍內,渦街流量計旋渦分離頻率對被測流體壓力、溫度、粘度和組分變化不敏感,在幾何相似和動力相似條件下可用一種典型介質(水或空氣)進行標定。基于這種認識,在對用于蒸汽計量的渦街流量計進行量值溯源時,同時受限于蒸汽實流檢測裝置運行成本高、安全性等因素,實際工作中通常使用水介質或者空氣介質代替蒸汽介質進行實流標定。但由于蒸汽介質具有高溫、高壓、可壓縮等特點,實際工作狀態與標定介質空氣或水相去甚遠。隨著渦街流量計在蒸汽計量領域越來越廣泛的應用,計量糾紛也不斷見諸報道,引起了人們的關注。
對渦街流量計在不同流體介質下的.計量特性以及影響潤街流量計計量特性的可能因素進行了大量研究。從謊體力學角度出發,根據相似原理分析了壓縮空氣代替蒸汽進行蒸汽流量計檢定的可能性。對渦街流量計進行了空氣和蒸汽實謊標定測試對比分析,結果表明兩者標定流量對比誤差為2.5%。對介圜溫度.介質雷諾數、檢定管道內徑與渦街流量計測量管徑不匹配、魔潤發生體尺寸改變等l起渦街流量計儀表系數變化的因素徹了分析。采用數值模報的方法研究了旋潤發生體形狀對渦街流量計中流動特性的影響,結果表明:聯蔚型發生體下游旋潤脫落穩定性更好,且斯特勞暗爾數飯流速(雷諾數)變化較小。國從可壓縮流體的流體力學方程出發對渦街流量計的流場進行了分析.將介圓可壓縮性對渦街流量計計量.特性的影響日結到流體等鶻指數x,得出介質可壓細性會造成儀表系數K值增大.且題介質來流速度的增大這種偏差逐漸增大,文章還通過實流測試和CFD仿真得到潤街謊量計在空氣和水介圈下的儀表系數偏差,驗證了理論分析。從渦街流量計儀表系數K的定義式出發總結出影響渦街流量計計量特性的主要因素為溫度和介質可壓餾性.為了直觀地顯示各變量可壓細性的影響程度.作者采用指數報合的方法以壓力p密度ρ和等嫡指數x為自變量得到了介質可壓縮性影響報合公式考慮到溫度對發生體形變的影響,l入材料線性酈脹系數描述溫度對儀表系數的影響,最后將這兩個因素綜合到一起得到系數修正計算方法。蘇慶文等國為了研究介圜可壓縮性對渦街流量計計量特性的影響,利用Fluent軟件對渦街流量計在蒸汽、空氣和水三種介圜下進行仿真研究,結果表明三種介圓下儀表系數從大到小依次為:空氣、蒸汽.水.說明空氣受介質的可壓細性影響最大.許文達等即對6臺不同口徑的渦街流量計分別在音速晴嘴法氣體流量標準裝置和冷凝稱重法蒸汽流量標準裝置上進行蒸汽和空氣介圜下的實驗研究結果顯示空氣介圈下的儀表系數整體上大于蒸汽介質下的值.
從目前對渦街流量計在不同介圜下的計量特性的相關研究來看,標定介質的可壓縮性、溫度以及雷諾數,旋渦發生體的幾何尺寸等是影響渦街流量計跨介質標定的主要因素,受此影響,采用空氣或水介質作為標定介質對蒸汽流量計量渦街流量計進行實流標定會產生一定程度的偏差。為保證蒸汽計量渦街流量計的計量可靠性、節約計量溯源成本、避免蒸汽貿易計量差額,有必要對渦街流量計在蒸汽介質.與空氣、水介質下的計量特性進行研究,分析渦街流量計跨介質標定影響因素的作用機理,并做出針對性修正。現有的相關研究中,針對渦街流量計在不同介質下的計量特性的實驗研究,測試流量點分布基本按照最大量程的不同百分比來劃分(如最大流量點的60%.40%等),這種簡單的對應關系沒有考.慮介質雷諾數的影響,缺乏理論支撐;一些研究人員從可壓縮流體遵循的物理方程出發,分析整理出與介質可壓縮性有關的變量,并進行了數值擬合得到介質可壓縮性理論擬合公式,這種理論分析計算結果與實流實驗數據存在--定偏差,不能完全滿足跨介質標定的系數修正的實際需求。
該文從渦街流量計基本原理出發,結合流體力學基本原理,研究介質可壓縮性對渦街流量計計量特性的影響,提出基于介質可壓縮性的儀表系數修正數學模型,最后對按照雷諾相似準則進行的實流實驗數據進行數值分析,通過最小二乘擬合得到儀表系數的可壓縮性修正公式。
1渦街流量計基本原理
1.1卡門渦街
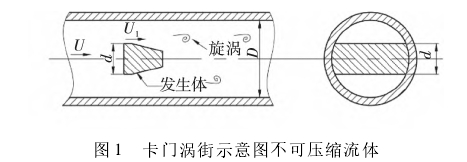
渦街流量計依據的基本原理為“卡門渦街”原理。具體來講,在測量管道中垂直地插入一-段非流.線型阻流體稱之為旋渦發生體,來流流體流過發生體,當管道內雷諾數達到--定值時,在發生體下游兩側會交替分離出規則排列的旋渦,這種現象稱為卡門渦街現象,如圖1所示。在一定雷諾數范圍內旋渦脫落頻率與發生體兩側的平均流速的關系可表示為中:

式中:ƒ為旋渦脫落頻率,Hz;Sr為斯特勞哈爾數;U1為發生體兩側流體平均流速,m/s;d為發生體迎流面的寬度,m。
測量管內的瞬時體積流量qv可表示為:

式中:qv為測量管內瞬時體積流量,m3/s;U為介質來流平均流速,m/s;D為測量管道內徑,m。
定義渦街流量計儀表系數K[1/m3]如下:

對于渦街流量計,斯特勞哈爾數Sr在一定管道雷諾數ReD范圍內為常數[10]由式(4)可知,渦街流量計幾何尺寸一定,在來流速度一定的情況下,在合適的管道雷諾數范圍內其儀表系數K僅與發生體兩側的平均流速U1有關,通常用儀表系數K來表征渦街流量計的計量特性。
1.2不可壓縮流體
對于不可壓縮流體,流體介質在流經發生體前后密度保持不變,根據流體連續性定理可得:
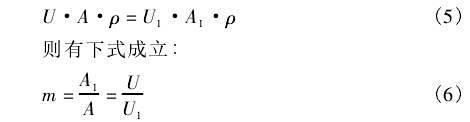
式中:A1為發生體兩側弓形區域面積,m2;A為管道橫截面積,m3;ρ為介質來流密度,kg/m3;m為發生體兩側弓形面積與管道橫截面積之比。
m的計算式為:
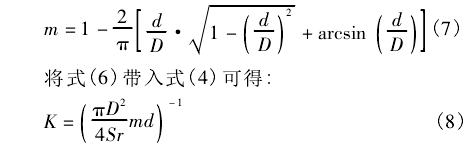
由式(8)可以看出,斯特勞哈爾數Sr--定時,對于不可壓縮流體介質,渦街流量計儀表系數K僅與渦街流量計幾何尺寸D、d有關,因此,在忽略介質可壓縮性影響的情況下,渦街流量計在不同介質下的標定結果具有通用性,這就是渦街流量計跨介質標定的理論依據。
1.3可壓縮流體
對于可壓縮流體,由于流體介質流經發生體前后密度發生變化,流動過程遵循以下方程:
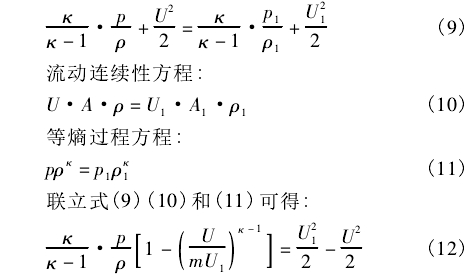
式中:K為流體等熵指數;ρ為發生體兩側介質密度.kg/m3;p為管道橫截面處介質壓力,Pa;p1為發生體兩側介質壓力,Pa。
式(12)描述了可壓縮流體介質來流速度U與發生體兩側介質平均流速U1的關系,可以看出兩者不僅與渦街流量計幾何尺寸有關,還與介質等熵指數、壓力、密度有關,且由式(4)己推知,渦街流量計儀表系數K與發生體兩側介質流速成正比。因此,若考慮介質可壓縮性的影響,則渦街流量計在不同介質下的通用標定性不再成立,即儀表系數不能簡單等同。
2可壓縮性修正數學模型
可壓縮流體在流經旋渦發生體時,其密度、壓力.會發生變化,這種由于流動截面突然改變導致流體介質參數發生改變的現象常見于流量測量和流動控制領域。例如利用流體流經節流件形成局部收縮,從而導致流速增加、壓力降低,在節流件前后形成壓差的差壓式流量計。受此啟發,該文參考介質可壓縮性對差壓式流量計的影響提出針對渦街流量計的可壓縮性修正數學模型。
該文選擇典型差壓式流量計--標準孔板流量計作為參考對象,理由是其發展時間久、理論研究充分。國際標準ISO5167-2:2003中n給出了針對可壓縮流體的標準孔板可膨脹性系數經驗公式:
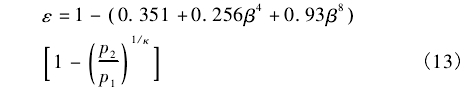
式中:ε為可膨脹性系數;β為節流孔直徑與測量管直徑的比值;p,為節流孔上游壓力,Pa;p2為節流孔下游壓力,Pa;K為流體等熵指數。
基于1.3中的理論分析,參考標準孔板的可膨脹性系數經驗公式,考慮渦街流量計幾何尺寸、壓力、等熵指數的影響,提出渦街流量計可壓縮性修正因子數學模型如下:
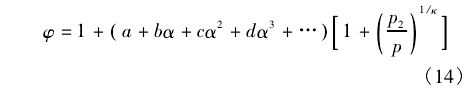
式中:Φ為可壓縮性修正因子;a,b,c,d為修正常數;α為渦街流量計幾何參數變量;p為介質來流壓力,Pa;p2為測量管道下游壓力,Pa。
類比標準孔板的等效孔徑比β的概念,提出渦街流量計幾何參數變量α.其幾何意義為渦街流量計有效流通面積與測量管道截面面積之比m的平方根,計算式為:

3數據擬合
為了求得上一節中提出的壓縮性修正公式,即解得修正常數a,b,c..,該文對實流標定實驗數據進行數值分析,采用離散數據擬合的方法12進行求解。
實驗選取水作為不可壓縮介質、空氣為可壓縮介質,以渦街流量計儀表系數K為修正目標提出以下修正公式:

式(17)中等號左側為關于幾何參數變量α的冪函數,a,b,c,d...為待求值,等號右側帶入實驗數據后為已知量,則儀表系數K的修正公式問題轉化為式(17)表示的線性擬合問題。帶入渦街流量計[13]在水和空氣介質下的實驗數據最終求得修正因子擬合公式如下:

4修正公式誤差及不確定度分析
4.1修正誤差分析
為驗證上述修正因子擬合公式的正確率,進行了誤差分析。誤差計算公式為:

式中:δ為修正誤差,%;K'gas為空氣介質儀表系數修正值,1/m3;Kgas為空氣介質儀表系數實驗值,1/m3。
四臺不同口徑實驗用渦街流量計儀表系數K的修正結果如圖2~5所示。
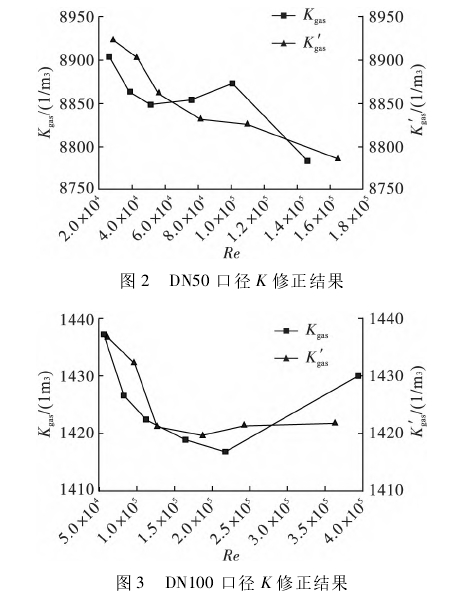
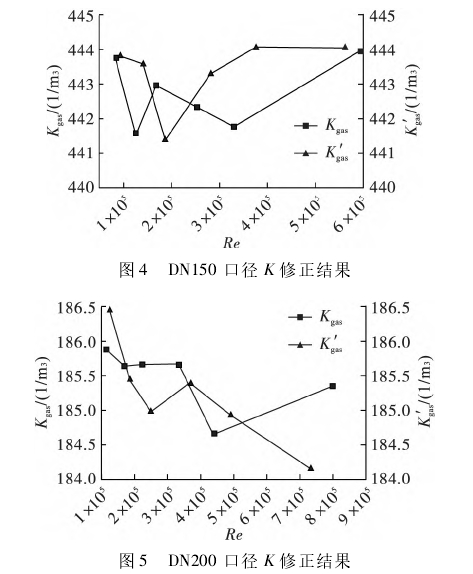
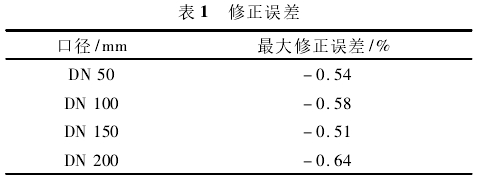
修正誤差計算結果如表1所示。
4.2修正公式不確定度分析
由第三節分析可知修正系數的不確定度輸入量包括:水介質儀表系數K的測量不確定度、發生體特征寬度d的測量不確定度、測量管內徑D的測量不確定度、壓力測量的不確定度等。則修正系數的相對標準不確定度的計算公式如下:
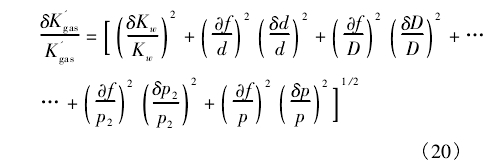
4.2.1水介質儀表系數K
水介質儀表系數K的測量采用靜態質量法水3流量標準裝置,其流量范圍為(0.2~680)rm3/h,測量擴展不確定度為Ur=0.029%,k=2,則:
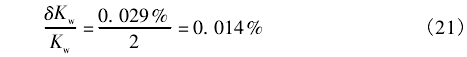
4.2.2發生體特征寬度d和測量管內徑D
發生體特征寬度和測量管內徑的測量采用激光跟蹤儀,查詢該裝置的校準證書得到其測量不確定.度為:UL=(0.5+0.3L)μm,h=2,則:

以DN50的分析結果為例,將各不確定度分量匯總如表2所示。
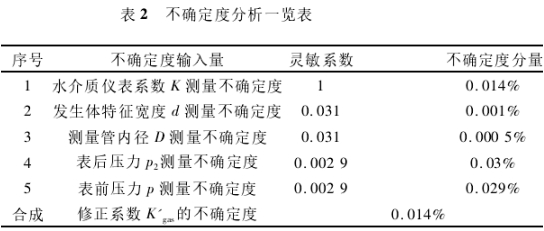
4.2.4擬合方法引入的不確定度
考慮曲線擬合法引入的不確定度提出擬合方法的不確定度計算公式如下:

式中:δI為各測試點的修正誤差,%;n為測試點個數;v為擬合常數個數(自由度)。
4.2.5合成標準不確定度
綜上,修正系數的合成標準不確定度為:

4臺不同口徑的渦街流量計的不確定度分析結果如表3所示。
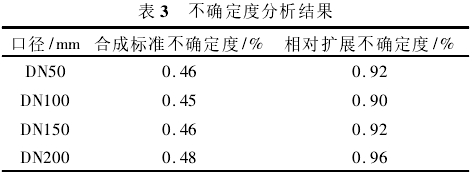
5結論
該文針對介質可壓縮性對渦街流量計儀表系數的影響,提出了基于介質可壓縮性的儀表系數修正數學模型,通過對水和空氣介質下的實流實驗數據的數值分析,擬合得到儀表系數的可壓縮性修正公式,最大誤差為-0.64%,相對擴展不確定度均在1%以內。該文的研究方法對于蒸汽介質渦街流量計的儀表系數標定具有指導意義,后續工作可針對水和蒸汽以及空氣和蒸汽之間的儀表系數修正開展。
本文來源于網絡,如有侵權聯系即刪除!