摘要:F雙鈍體旋渦脫離的流體動力學特性以及利用雙鈍體增強流體振動的最佳組合結構。給出了多種鈍體組合結構的斯特勞哈爾數的試驗結果,表明雙鈍體結構具有常定的斯特勞哈爾數。用50mm口徑渦街流量計進行的試驗證明,雙鈍體組合在一定的條件下能獲得理想的旋渦重疊,從而增強流體的振動。在鈍體的軸對稱點上,還觀察到強度和頻率相同,相位相差180°的流體振動點,利用優化的雙鈍體結構和差動傳感技術,研制出小流量靈敏度和抗干擾性能很好的新型旋渦流量計。
0前言
斯特勞哈爾和馮·卡門對鈍體繞流所做的開拓性研究揭示了旋渦脫離的基本特征和規律,即:當流體流經鈍體時,尾流中將形成旋渦流型,旋渦從鈍體兩側交替地脫離,并在---個較寬的雷諾數范圍內,有常定的量綱一的脫落頻率,即斯特勞哈爾為常數。這表明旋渦脫落的頻率與平均流速成正比。
Roshkol21的研究給出了更為明確的結果,即在雷諾數處于300<Re<2X105的范圍內時,斯特勞哈爾數保持在0.2左右,他還首次提出了利用斯特勞哈爾數的常定范圍來制造流量計的設想。20世紀70年代初,商品化的渦街流量計在日本出現。近30年的工業應用證明了渦街流量計在穩定流體計量中的可靠性和精確性,它的主要優點還包括精度高、線性度好、介質適應性寬和性能可靠(無運動部件)3]。然而,渦街流量計存在的流量下限高和抗干擾性能差等問題,使它喪失了許多潛在的應用領域,如:量大面廣的天然氣商業計量以及流速和壓力不穩定的測量系統。
為了將渦街流量計應用于不穩定流體的計量,本文利用鈍體組合強化旋渦脫落誘發流體振動的理論研究基礎上,設計出雙鈍體渦街流量計試驗樣機:通過試驗獲得了雙鈍體的最優組合結構及參數;分析了鈍體組合對斯特勞哈爾數的影響;同時在后鈍體的軸對稱點上,還觀察到強度和頻率相同,相位相差180°的流體振動點,這些研究結果為研制具有良好抗干擾性能和小流量靈敏度的雙鈍體差動式渦街流量計提供了依據。
1雙鈍體渦街流量計的原理
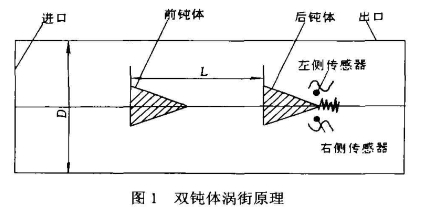
雙鈍體渦街流量計的基本設計思路是利用前鈍體和后鈍體引發的旋渦脫離現象,通過試驗獲得使旋渦在后鈍體周圍實現同相位疊加的最佳鈍體組合,使流體振動得到加強,降低計量的下限,同時利用鈍體兩側的流體振動具有180°相位差的特點,用差動式傳感器抑制共模干擾信號的方法,提高流量計的抗干擾性能,圖1所示為雙鈍體渦街流量計的原理。
2試驗裝置
圖2所示為試驗裝置及測試系統原理。
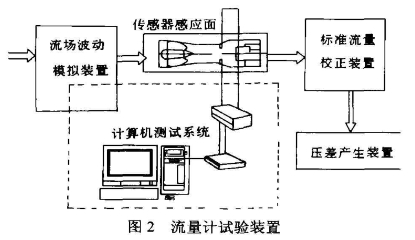
試驗裝置為氣體流量試驗系統,它由5個部分組成。I一流場波動模擬裝置,用于實驗室條件下模擬流場波動;II一試驗表體;II一標準流量校正裝置,本試驗臺采用臨界流文丘利噴嘴流量計作為校準其他儀表的基準;IV一負壓產生裝置,本試驗臺通過真空泵產生負壓,使試驗臺的入口和出口之間產生一個壓差,這樣就形成一個小型風洞。真空泵電動機額定功率為11kW,額定轉速為1450r/min;V一計算機測試系統,主要由電荷放大器、DAC-TRON公司Photo便攜式動態信號分析儀(該分析儀的主要特性和性能指標:4個輸入通道,一個輸出通道;120MHzTMS320VC33DSP,21kHz處理率;32位浮點DSP;ICP傳感器供電;USB接口,支持熱插拔;質量小于200g,抗振動外殼)及計算機所組成。
試驗臺的臨界流文丘利噴嘴測定裝置由5個標準的不同噴嘴流:量計組成,通過不同的組合方式可得到5.5--220.5m³/h之間的流量。試驗的管道內徑50mm。
3試驗結果
試驗分為兩個部分,1一雙鈍體組合渦街振動頻率試驗;2一雙鈍體組合方式對渦街強度的影響。試驗傳感器如圖1所示對稱于后鈍體安裝。試驗表體直徑為50mm。
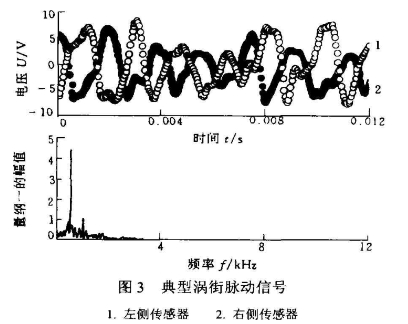
典型的渦街脈動信號如圖3所示。從信號的時域信號可以看出。對稱于后鈍體兩側渦街的脈動是反相的,并有明顯的周期性,其功率譜的頻率分布很廣并有一個明顯的峰值,該峰值處頻率和時域信號的主波動是頻率是相同的。定義功率譜中該峰值處的頻率為渦街的主頻。下面所討論的渦街頻率指的就是渦街的主頻。
3.1雙鈍體組合渦街振動頻率試驗研究
對于單鈍體渦街,在臨界雷諾數之上斯特勞哈爾數是恒定的,這是單鈍體渦街流量計的測量基礎。雙鈍體渦街是否存在同樣的規律是雙鈍體渦街流量計的關鍵。本部分的試驗研究是為尋找當旋渦發生體是兩個三角形時渦街的斯特勞哈爾數是否發生變化。本部分的另一個目的是研究鈍體的平行組合對渦街斯特勞哈爾數的影響。
試驗所用雙鈍體組合圖1所示,圖中的前后.鈍體的互相平行的,鈍體的組合方式是指兩個鈍體之間的距離不同情況的組合。
試驗的設計是對相同的鈍體組合在不同的流量情況下進行試驗。以得到不同組合下不同流量的測量數據。試驗的采用數據如表所示。
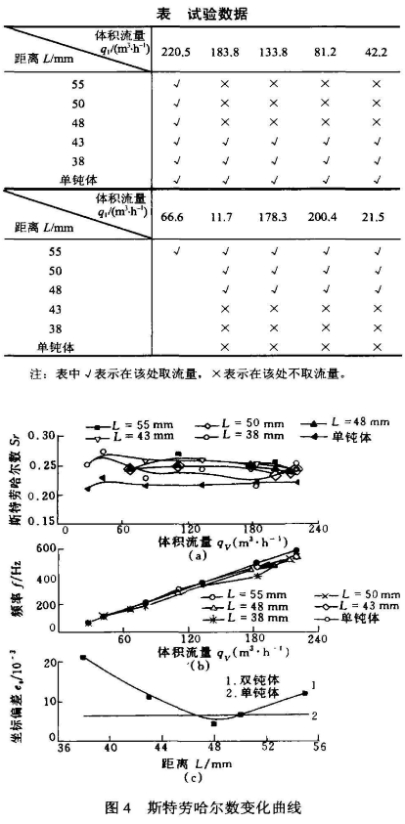
流量的選取不少于5個點,并通過流量不完全相同的選取來達到覆蓋較多流量范圍的目的。圖4a為試驗所得的各組雙鈍體和單鈍體斯特勞哈爾數;圖4b是流量和渦街頻率的關系曲線:圖4c為各組雙鈍體和單鈍體斯特勞哈爾數標準偏差曲線。
從圖4a和圖4b中可以得出如下結論。
雙鈍體的斯特勞哈爾數比單鈍體斯特勞哈爾數大,不同組合雙鈍體的斯特勞哈爾數是不相同.的。不同的雙鈍體組合的斯特勞哈爾數的波動不相
同的,其斯特勞哈爾數的標準偏差如圖4c所示。從圖4c中可以知道,雙鈍體的斯特勞哈爾數波動是比較大的,在L=50~46mm之間偏差與單鈍體偏差相當。
由4b圖,該曲線的線性度與斯特勞哈爾數標準偏差相對應,當L=50~46mm時雙鈍體流量--頻率曲線的線性度較好。
綜上所述,對于雙鈍體渦街流量計從測量的線性范圍角度考慮應選擇L=50~46mm之間的組合方式。
3.2雙鈍體組合方式對渦街強度的影響
上面得出雙鈍體流量計最佳線性范圍條件。流量計的另-一個重要的問題是渦街強度,其直接影響測:量信號的信噪比。其對降低量程下限有重要的意義。
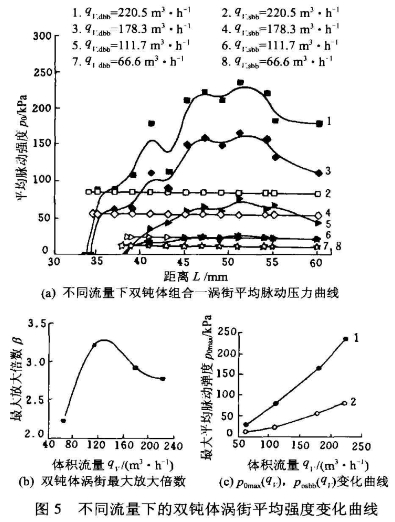
為研究雙鈍體組合對渦街強度的影響。設計了如下試驗。試驗裝置如圖1所示;通過改變距離L對鈍體進行組合并對該組鈍體在不同流量下進行試驗。試驗所使用的流量是220.5m3/h,178.3m'/h,111.7m3/h,66.6m3/h等4組。使用的鈍體組合有L=60mm,55mm,54mm,51mm,49mm,47mm,45mm,43mm,41mm,39mm,37mm,35mm,33mm,32mm,29mm等15個組合。
進行強度比較之前,需要對渦街的信號特點進行分析并定出可以度量強度的量。如圖3渦街信號是周期性的但其波動的幅值不等,故渦街的強度需要從統計.上進行比較。試驗中制定的渦街強度的統計量為.

這里`y表示的是脈動壓力信號平均的波動幅值,通過換算可得到渦街的平均脈動強度。以后的所有有關強度比較都是以`y為的度量。
圖5a是試驗得到渦街的程度在不同組合在不同流量下的比較曲線,圖上的P0是通過`y換算而.來的,可以認為是渦街的平均脈動強度。
圖5b是不同流量下的渦街平均脈動強度最大的放大倍數,這時定義

從不同組合在不同流量渦街強度比較曲線可以得到以下結論:
雙鈍體對渦街的強度有加強的作用。在不同的流量下雙鈍體對渦街的加強程度是不一樣的如圖6a所示。從qv---β可以知道在不同流量下渦街平均強度最大的放大倍數是不相同的,β在qv=130m3/h時達到最大。
P0隨L非線性變化,在L=45~54mm之間P0梯度很小,即在該區域內L的變化對渦街強度的影響不顯著。
渦街的強度有一個峰值區域。當偏離這個區域后渦街的強度發生明顯的衰減。該峰值區域與較小P0梯度區域重合。
相同流量下,雙鈍體渦街強度始終比單鈍體渦街大。在流量不變情況下,當雙鈍體渦街強度接近單鈍體渦街強度時,微小的L變化會導致雙鈍體卡門渦街現象的消失,即存在一個產生雙鈍體卡門渦街的臨界距離Le,且Le與流量有關,在Le處雙鈍體渦街強度和單鈍體渦街強度相等。當L<Le該流量下雙鈍體卡]渦街現象將消失。但Le是否與尺度相關需要進一-步的研究。同樣隨L不斷增長是否也存在一個臨界距離也需要進一步研究。
4結論
通過上述的試驗研究,可以得出以下的結論:用雙鈍體誘發卡門渦街可以增強渦街的脈動平均強度,有利于提高測量的信噪比,降低渦街流量計的測量下限。最大強度鈍體的組合L=45~-54mm。
通過適當的選擇鈍體的組合,雙鈍體渦街流量計的精度和單鈍體渦街流量計是相當的。最佳線性度鈍體組合為L=46~50mm。
綜上述,通過兩個三角型鈍體組合可以得到與單鈍體渦街流量計測量精度相當但信號信噪比高、測量下限較低的雙鈍體渦街流量計。雙鈍體的最佳組合方法是L=45~50mm之間。
本文來源于網絡,如有侵權聯系即刪除!






