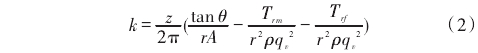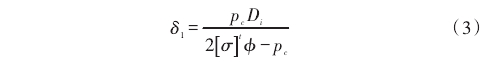摘要:為了使渦輪流量傳感器能保證在氣體、黏性介質和小流量等流體條件下有測量性能,目前科技工作者對泥漿渦輪流量計結構的優化與改進做了大量的研究工作,但主要研究集中于傳感器葉輪、軸承、非磁電信號檢出器等部件的改進與優化方面。由于渦輪流量計內部幾何參數較多,各參數對流量計精度影響.的機理也各不相同,并且各參數之間存在一定的交互作用,所以本文從各參數的交互作用出發,對渦輪流量.計結構參數進行了優化,研究各參數對其性能的影響,并利用CFD(計算流體動力學)進行仿真,探究各參數的作用機理,得到一組組合。仿真結果表明,儀表系數線性度誤差由原來的5.23%降低到4.69%,流量計測量精度顯著提高。
渦輪流量計是一種廣泛應用于工業生產的流量計量儀表。當被測流體流過渦輪流量計內部的葉輪時,流體沖擊葉輪,葉輪發生旋轉。流量不同時,流體通過同一截面的流速就不同,對葉輪的沖擊力也不同,造成葉輪的轉速也不同。通過標定,用測量葉輪轉速的方法來測量流體介質的流量。這種流量測量方式具有精度高、重復性好、量程范圍寬、輸出脈沖信號抗干擾性強的優勢,在航空航天燃料計量、天然氣計量、油品計量和貿易結算、工業生產過程監控等領域廣泛采用”,但在計量黏度較高的流體時,其線性度降低,結果誤差較大。為了計量高黏度流體而不得不采用渦輪流量計時,必須對具體的介質進行專門設計。為了計量固井泥漿。
1泥漿渦輪流量計的幾何參數計算
渦輪流量計的基本結構如圖1所示。
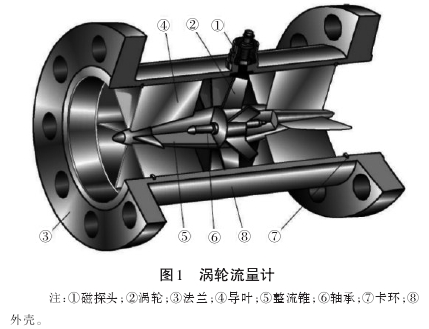
當流體通過渦輪流量計時,流體動能使葉輪旋轉,流體流速越快,動能越大,葉輪轉速也越高。因此,測出葉輪轉數或轉速,就可測量流過管道的流量。傳感器將流量Q轉換成葉輪轉速ɷ,信號檢出器把轉速ɷ轉換成脈沖信號頻率ƒ,送入二次儀表進行顯示和計數。單位時間內的脈沖數和累積脈沖數分別反映了瞬時流量和累積流量。由于渦輪流量計的轉速以頻率信號輸出,所以可制成數字儀表,也便于與數控裝置相配合。
通過流量計的流量和葉輪引起的頻率關系為:
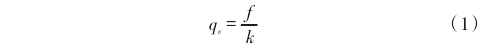
式中;qv表示瞬時體積流量;ƒ表示脈沖頻率;k表示儀表系數。
對于結構參數確定的渦輪流量計,在其穩定運行后,不同的流量對應唯--不同的轉速和頻率ƒ。因此,影響流量計精度的主要因素為儀表系數,其表達式為:
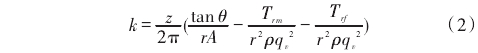
式中:z表示葉片數;θ表示葉片傾角;r表示葉輪半徑;A表示過流面積;ρ表示液體密度;qv表示瞬時體積流量;Tm表示摩擦力矩;Trf表示流動阻力矩。
儀表常數特性曲線如圖2所示。從圖2可以看出,儀表常數的線性范圍與標定系數K。的關系直接影響著流量計的精度。
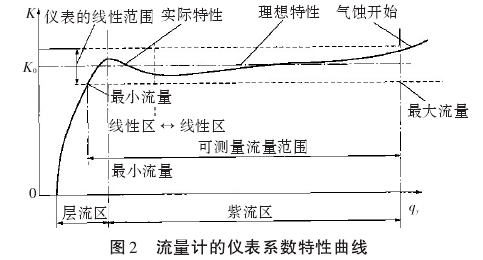
流量計設計的初始參數如下:流量計公稱內徑為.101.6mm,流量范圍0~3m³/min,工作壓力40MPa,鉆井液密度1.2~1.3kg/m³,黏度50~60cSt。
渦輪流量計材料選用0Cr18Ni9不銹鋼,考慮到工作壓力為40MPa,設計壓力p≤0.4[σ]'φ,按厚壁圓筒進行計算,根據中徑公式和第一強度理論得出相應的筒體厚度為:
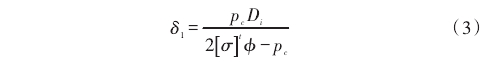
其中,D,表示圓筒內徑,mm;pc表示計算壓力,MPa;[σ]表示設計溫度下圓筒材料的許用應力,MPa;φ表示焊接接頭系數。
為了方便選取渦輪流量計參數,同時考慮到渦輪流量計的國家標準,選取公稱外徑為101.6mm的渦輪流量計,其余參數按經典取值表進行取值[5-1,其中葉片頂端間隙與管道半徑之比t=2.0097,葉輪輪轂半徑與葉輪葉片頂端半徑之比q=0.495,葉片均方根平均半徑位置的安裝角b=42.38°,葉片頂端處葉柵具有的實度s=1.254。
渦流流量計葉輪部分結構參數如圖3、圖4所示,其中Rk為葉輪輪轂半徑,mm;L為葉輪輪轂長度,mm;Rt為葉輪葉片頂端半徑,mm;R0為流量計管道半徑,mm;R1為葉輪旋轉軸半徑,mm。
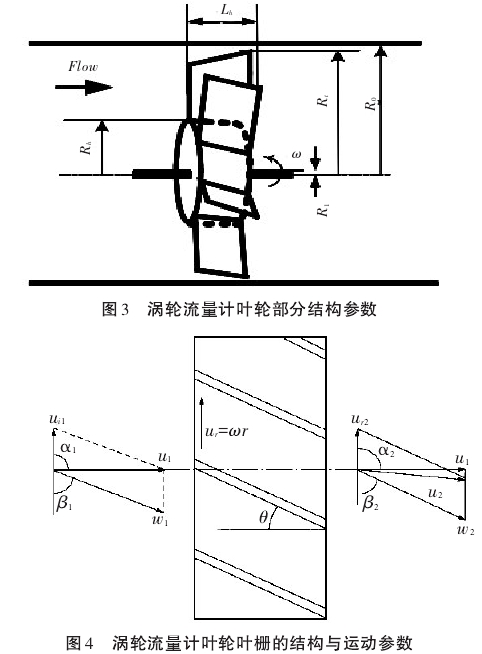
流量計口徑大小不同,葉片數量也應不同。小口徑的流量計(D≤100mm),葉輪葉片數量通常為3~8片;大口徑的流量計(D>100mm;),葉輪葉片數則通常為10片以上5。根據流量計設計準則得出的參數如表1所示。

根據以上參數建立流量葉輪與導葉的三維模型如圖5所示。
2泥漿渦輪的仿真分析
2.1網格劃分
將三維模型導人ANSYSICEM中,在ICEMCFD中將葉輪流域和導流件流域部分采用非結構化的四面體網格進行劃分,前、后直管段流域均采用結構化的六面體網格進行劃分。如圖6所示,其網格質量的最小值為0.34,大于0.3,滿足網格質量要求。

2.2邊界條件
第一,仿真介質為實際狀況下的油,其運動黏度為50cSt,密度為1.3kg/m3,流量范圍為20~200m3/h,流量點分別取為:2、4、8、14m3/h和20m3/h。
第二,人口采用速度人口,通過具體的流量值、流體密度和傳感器管道口徑便可以計算出傳感器的人口速度。
第三,出口采用壓力出口,設置為一個標準大氣壓。第四,管壁,上、下導流體和葉輪表面均采用無滑移壁面邊界條件
第五,為更好地模擬渦輪流量計在復雜流場狀況下的運行規律,選用RSM湍流模型2.3模型仿真儀表系數
模型測量流量點與儀表系數關系如表2和圖7所示;
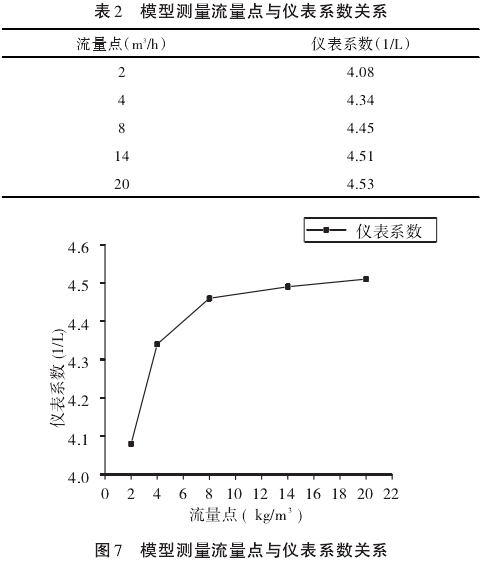
從圖7可知,渦輪流量計線性度誤差為5.23%,且在小流量處的儀表系數變化很大,在大流量時較為平穩。
2.4幾何參數對儀表系數的敏感性分析
渦輪流量計葉輪部分幾何結構對測量精度影響很大。。本文選擇模型流量計葉輪部分的幾何參數(葉輪葉片頂端半徑、葉輪輪轂半徑、葉輪輪轂長度、葉片導程),通過單因素試驗設計,即改變某--幾何參數的結構尺寸的同時保持其余各參數不變,選取2、4、8、14m'/h和20m/h五個流量點進行仿真,以渦輪流量計儀表系數的線性度誤差作為判斷依據分析上述葉輪四個幾何特征的敏感情況。仿真結果如圖8至圖11所示。
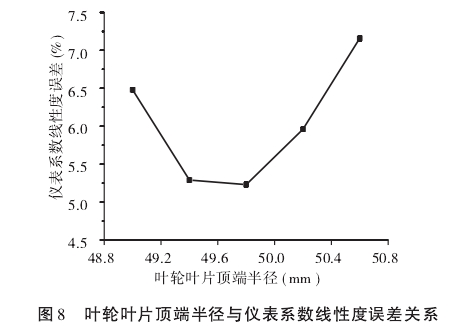
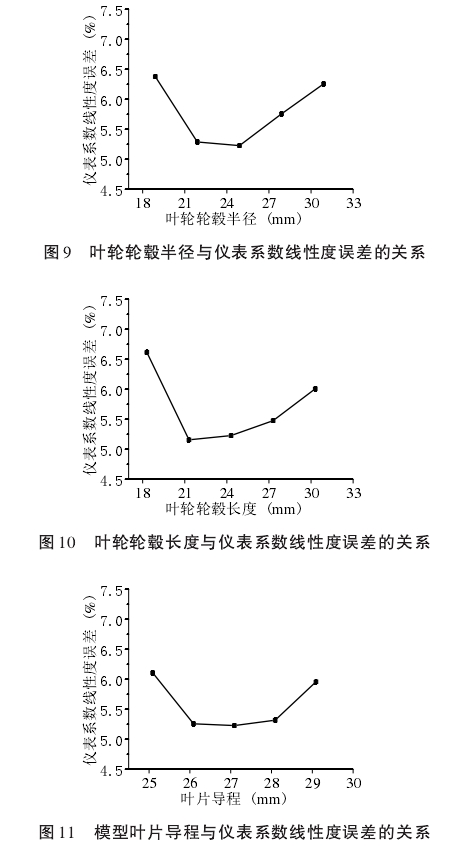
仿真結果顯示,在單--改變某幾何參數的情況下,均存在最優值,使得儀表系數線性度誤差達到最小。
3泥漿渦輪流量計的優化設計
采用Box-Behnken中心組合設計方法,以葉輪葉片頂端半徑、葉輪輪轂半徑、葉輪輪轂長度、葉片導程這四個因素為自變量,流量計線性度誤差為響應值,設計四因素三水平29個試驗點的響應面優化試驗。因素水平見表3。
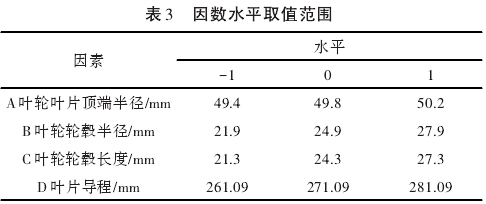
使用DesignExpert軟件在表3中變量的高低水平范圍內尋優,取其中1個最優組合如表4所示,對其進行CFD計算,并與響應面回歸方程的預測值和原始流量計儀進行比較[10]。,優化前后流量計參數如表5所示,優化前后的結果如圖12所示。
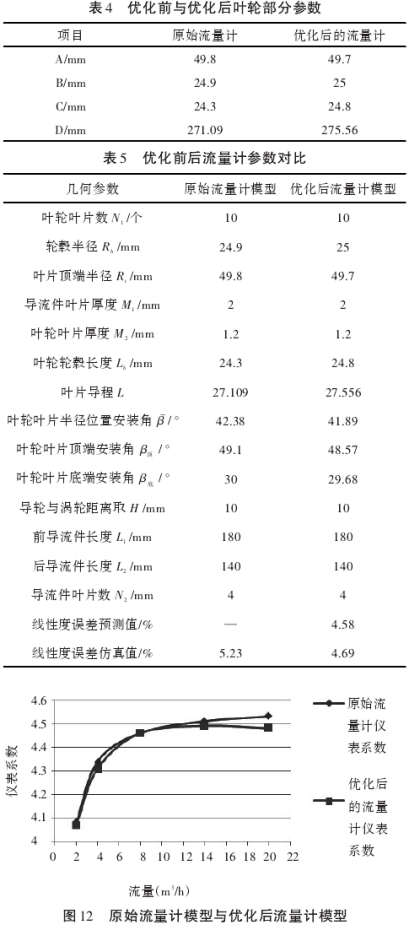
從仿真數據得到,優化后的流量計模型,其儀表系數線性度誤差由原來的5.23%降低到4.69%,擬合公式的預測值也與CFD計算值非常接近,為2.18%,這表示響應面法可以很好地用于渦輪流量計結構參數優化。從圖12可以看出,優化后的流量計雖然在小流量處時儀表系數變化還是很大,但是在測量8~20m³/h流量時,其儀表系數變化較原始流量計更為平穩,且線性度誤差為0.447%。這表明該流量計在測量流量為8~20m³/h時,該種流體時精度很高。
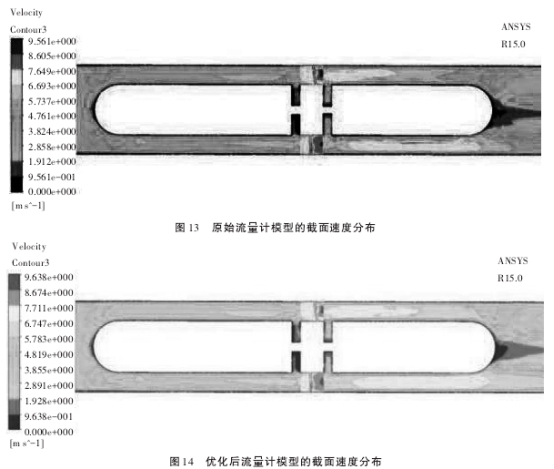
從圖13可以看出,原始流量計模型受流體密度和高黏度的影響,速度分布不太均勻,且后導流件部分存在速度增大較為嚴重的情況,不利于流量計測量的提高。從圖14可以看出,優化后的流量計整體速度分布更加均勻,后導流件部分沒有速度增大較為嚴重的情況出現,這表明優化后的流量計模型提高了流量計的測量精度。
4結論
本文針對固井中的特殊工況,采用渦輪流量計計算公式,,對公稱直徑為101.6mm、葉片數為10的渦輪流量計的結構參數進行了重新設計,得到--組更適用于固井泥漿計量的結構參數。同時,利用CFD軟件分析了流量計內流場特征,分析了不同葉輪幾何參數對儀表系數的敏感性。仿真結果表明,在一定范圍內,各幾何參數分別存在一個優值,使儀表線性度誤差最小。最后,采用Box--Behnken中心組合設計方法對渦輪流量計進行結構參數優化,在各參數的高低水平范圍內尋優,最終得到一個組合,優化后的流量計在固井泥漿計量中測量精度顯著提高,儀表系數變化更加平穩,其線性度誤差明顯降低,速度分布也更加均勻。
本文來源于網絡,如有侵權聯系即刪除!