摘要:介紹了渦街流量計原理,研究了渦街信號處理方法,設計了IIR和FIR數字濾波器,并用圖形化編程軟件Lab-VIEW進行仿真實驗,觀察了數字濾波器在渦街信號處理中的效果。
1渦街流置計
流量計量是計量科學技術的組成部分之一,它與國民經.濟、國防建設、科學研究有著密切的關系,隨著我國工農業的發展,對流體流量的計量提出了越來越多、越來越高的要求,特別是在注重節省能源、提高經濟效益和產品質量的今天,流量計量與測試的重要性就更加突出了,并且為越來越多的人所認識。在氣體、液體、蒸汽的流量測量中,渦街流量計具有精度高量程比較寬、線性度較好、壓力損失小、性能可靠、測量元件結構簡單、使用壽命長、安裝維護方便、適用各種介質等一系列的優點,在計量檢測中發揮越來越大的作用,有著廣泛的應用前景。
2渦街信號研究
理想情況下,渦街流量傳感器的輸出信號應該是正弦波,其頻率與流體的流速成正比。然而,工業現場的噪聲是普遍存在的,這些噪聲信號包括管道內流動介質的湍流、脈動、流場的不穩定及不均勻性對渦街發生體施加不規則的附加作用力而產生的流體流動噪聲。當規則渦街產生后,在工作信號上會迭加一種1/5到1/10渦街頻率的流體低頻擺動噪聲,或輸送流體的管道偶爾受到外力撞擊,會產生隨機振動噪聲;以及各種.動力源,如水泵、壓縮機等的振動由管道傳遞到傳感器上,造成渦街發生體上產生附加的慣性應力,形成的振動噪聲。因此,實際的渦街傳感器的輸出信號遠非理想的正弦波信號,而是一個混有強噪聲的混合信號,它是由兩部分信號組成:一是流速產生的渦街信號S(t),二是干擾引起的噪聲信號N(t),即實際的渦街信號Y(t)=S(t)+N(t),其中噪聲信號中又含有確定性分量和隨機分量。隨機分量可認為是服從高斯分布的白噪聲信號,而確定性分量是由流體低頻擺動或動力源振動引起,獨立于渦街信號,可由另-一個正弦信號來模擬。因此,渦街傳感器的輸出信號Y(t)可以用下面的式子近似表示:
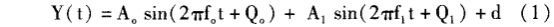
式中:Ao,fo,Q。分別表示渦街信號S(t)的幅值、頻率和初始相位;A1,f1,Q1分別表示噪聲信號N(t)中諧波干擾分量的幅值、頻率和初始相位;d表示噪聲信號N(t)中的高斯分布白噪聲會疊加在渦街信號中,使測量結果產生較明顯的誤差。所以,選用適當的數字信號處方法去除信號中噪聲的干擾,最大程度的復現流速信號,是進行渦街信號處理的主要任務。
3數字濾波器的設計
用窗函數法設計FIR數字濾波器就是用有限長的脈沖響應序列來逼近無限長的脈沖響應序列。基本設計思想為:首先選定一個理想的選頻濾波器,然后截取它的脈沖響應得到線性相位和因果的FIR濾波器。因此,這種方法的重點是選擇-一個合適的窗函數和理想濾波器。一個理想低通濾波器的頻率響應為:
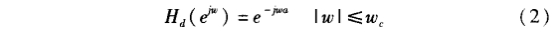
其中,;wc是濾波器的截止頻率,a為采樣延遲這個濾波器的脈沖響應具有無限持續時間,它由下式給定:
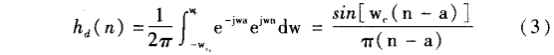
注意,hc(n)關于a對稱,這一點對于線性相位濾波器是有用的。
為了從hd(n)得到一個FIR濾波器,必須同時在兩邊截取hd(n)。而要得到-一個因果的線性相位濾波器,且它h(n)的長.度為M,這種操作叫做“加窗”,則h(n)可以看作是hd(n)與窗函數w(n)的乘積:根據w(n)的不同定義,可以得到各種不同的窗結構,包括矩形窗、三角型窗、漢寧窗、海明窗、布萊克曼窗等,這里采用的是海明窗進行FIR數字濾波器的設計。海明窗這種窗函數是漢寧窗的一種變形,它的形狀也相似于一個余弦曲線。可定義為:
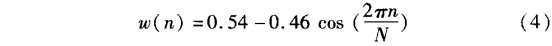
窗函數設計FIR濾波器的步驟:
1)根據技術要求確定待求濾波器的單位取樣hd(n)。如果給出待求濾波器的頻率響應為Hd(ejw),那么單位取樣響應用下式求出:

2)據對過渡帶及阻帶衰減的要求,選擇窗函數的形式,并估計窗口長度n。
3)計算濾波器的單位取樣響應h(n)。
4)驗算技術指標是否滿足要求。設計出的濾波器頻率響應用下式計算:
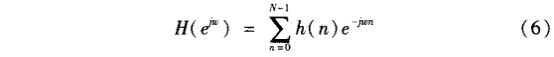
計算上式時可以用FFT算法。如果H(ejw)不滿足要求,根據具體情況重復2,3,4步,直到滿足要求。
流速信號中存在大量的噪音干擾信號,由管道振動、外界振動引起的干擾信號,還有50Hz交流電的干擾信號,真正的現場存在的干擾要比這些強得多,也就是使用捕捉數字脈沖的檢測方式不能檢測出低流速下的信號,這些信號都對流速的測量,特別是低流速的測量產生很壞的影響。所以必須對原始信號進行處理。從數字濾波前后的流速信號波形對比可以看出,濾波后的波形要平滑的多,也就是將大部分的噪音信號去除了,這樣就可以方便進行計算,得出流速值。從數字濾波后的波形圖可以看出,IIR濾波和FIR濾波都能夠達到不錯的效果,都可以完成流速信號的檢測,可以根據它們的適用場合和適用條件不同,決定選用具體的濾波方法,達到檢測流速信號的效果。
本文來源于網絡,如有侵權聯系即刪除!