摘要:電磁流量計在工農(nóng)業(yè)及民生領(lǐng)域的流量計量中應(yīng)用廣泛,而電磁流量計的精度主要依靠自身的測量精度而不易受介質(zhì)影響。使用多電極電磁流量計,旨在從流量計的多電極電勢差角度出發(fā)提精度。基于電磁感應(yīng)原理與權(quán)函數(shù)理論,提出一種改進的截面劃分方法,通過COMSOLMultiphysics進行仿真,得出電極間的電勢差。使用吉洪諾夫正則算法對速度矩陣進行求解,得出速度重構(gòu)值。仿真與計算結(jié)果表明,該設(shè)計合理正確,仿真得到的感應(yīng)電動勢在截面處的速度分布符合理論分析,速度的理論值與重構(gòu)值的誤差不高于1.50%,顯著提高了電磁流量計測量的魯棒性與精度。
流體在管道內(nèi)的流動工況普遍存在于冶金、能源和化工等眾多領(lǐng)域,流速的測量作為工況中的一個重要指標,其精度對生產(chǎn)過程中流量的測量以及控制與優(yōu)化都具有重要的實際意義”。
電磁流量計依據(jù)法拉第電磁感應(yīng)定律制成,由于其內(nèi)部沒有阻礙流體流動的擾動件,而且測得的速度值與流體自身的物理參數(shù)無關(guān),故廣泛應(yīng)用于化工、醫(yī)藥工業(yè)以及各種強腐蝕性、易爆易燃漿液的流量測量日。例如,在負擔供水任務(wù)的水庫管理中統(tǒng)計每天的放水量是一件非常重要的工作田,傳統(tǒng)的單對電極計量被普遍用于測量導電流體的流量。國內(nèi)采用--對電極的高精度中小管徑的電磁流量計的精度級別達到0.2。然而,它只適用于中小管徑且軸對稱流的情況,在非軸對稱流或者非滿管情況下,其測量誤差較大。實際情況中,只有當被測管道足夠長時(為5~10D,D為截面直徑),管道流型才會發(fā)展為充分發(fā)展流,當流速較快時,管道內(nèi)流型是不穩(wěn)定的,在管道上部會有波浪產(chǎn)生,無法通過單對電極測出正確的流速。而多電極計量可從不同電極對獲得多組電勢差,故可以提高非滿管與非軸對稱流量的測量精度用。
自1962年Shereliff給出兩電極權(quán)重函數(shù)的表達式以來,隨著科學技術(shù)的發(fā)展,多電極技術(shù)取到了長足的進步。然而其實現(xiàn)過程中存在--定困難,主要原因是劃分區(qū)域過小、矩陣計算時間過長、制作成本和難度較高。國內(nèi)尚不能提供擁有自主知識產(chǎn)權(quán)的產(chǎn)品。本文設(shè)計了一種8電極電磁流量計,并提出了一種改進的區(qū)域劃分方法,運用COMSOLMultiphysics進行有限元仿真得出電勢差,由于權(quán)函數(shù)理論公式針對8電極電磁流量計沒有精確解,故采取吉洪諾夫正則化方法,通過Matlab實現(xiàn)流場速度分布的不適定重構(gòu)求解。
本文在前人研究的基礎(chǔ).上,對電極數(shù)量與區(qū)域劃分重新改進,旨在降低速度的重構(gòu)值誤差。與更多數(shù)量電極相比,該方法復雜度較低,在保證系統(tǒng)實時性較好的前提下,在非對稱流、非滿管的情況下仍可維持較高精度。
1多電極電磁流量計設(shè)計
1.1多電極流量計測量的理論基礎(chǔ)
在對電磁計量求解Maxwell方程組時,需要設(shè)定.電勢U在流量計界限處的前提條件:管道內(nèi)充滿介質(zhì);管道與外部絕緣,即管道壁上不存在法向電流。在實際測量中,假設(shè)磁感應(yīng)強度B僅在x軸方向分布即B=Bx,流體介質(zhì)按軸向流動υ=υx。因此在忽略湍流的情形下,電極A與電極B之間的電勢差UAB;可表示為
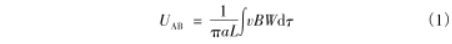
式中,α為管道內(nèi)壁半徑;L為電極對的直線距離;υ為流體速度;W為權(quán)重函數(shù),只與電磁流量計結(jié)構(gòu)相關(guān);積分域T實際指所有流動的流體,因為其他方向。上速度為0,對積分沒有貢獻。
對于多電極電磁流量計而言,電極位置按一定的規(guī)律遍布在管道內(nèi)壁,測得的感生電勢有多組。如果將電極所在處的整個管道橫截面劃分成尺寸極小的N個測量區(qū)域,假設(shè)沿管壁布置i對測量電極,當介質(zhì)流過橫截面時,每對電極都得到一弦端電壓U,管道切面處第n個區(qū)域?qū)Φ趇對電極上得到的電勢權(quán)重值記作Wn.t,則式(1)可變換為
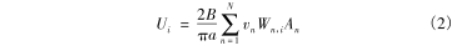
式中,N為切面所劃分的區(qū)域個數(shù);α為管道內(nèi)壁半徑;B為切面處的平均磁感應(yīng)強度;υn為第n個區(qū)域內(nèi)的軸向平均速度;An為該區(qū)域的面積大小:Wn.i為第n個區(qū)域?qū)Φ趈對電極間獲取的感應(yīng)電動勢的權(quán)重函數(shù);Ui為第i對電極間的電勢測量值。
1.2電極設(shè)計與區(qū)域的劃分
在使用多電極電磁流量計進行流量檢測時,電極數(shù)目的選擇至關(guān)重要。數(shù)目增多可提高測量精度,但是制作成本與制作難度會大幅提高,計算時間也會不可避免地增加,而若數(shù)目太少,數(shù)據(jù)精度較低,意義不大。故本文采用了一種8電極電磁流量計,旨在提高測量精度的同時保證時效性與成本。
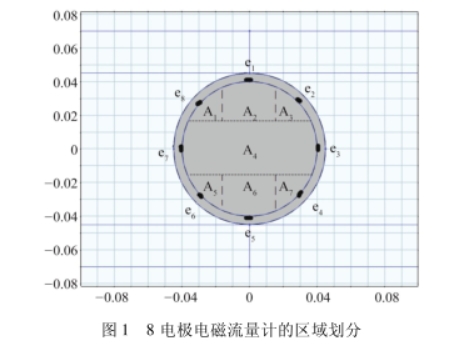
針對8電極電磁流量計采用了一種平行布置區(qū)域的方式,在8對電極的情況下劃分出3個區(qū)域,每個區(qū)域內(nèi)相對應(yīng)的電極處于該區(qū)域的中心位置。然而,這種劃分方法只能得出同一水平高度的平均流速,無法在垂直于洛倫茲力的方向進行更精細的劃分,分辨率較低。因此一種分辨率更高的劃分方法。將8個電極間隔45°安裝在被測截面內(nèi)壁上,電極分布如圖1所示,e1~e8依次表示8個電極。以電極為界限,進行豎直方向的劃分,相應(yīng)地會得到7個感應(yīng)電勢差,對應(yīng)有7個求解區(qū)域’。如圖1所示,從上往下將測量區(qū)域依次分成A1~A7。其中面積比較大的A.區(qū)域是被測對象橫截面積最大的區(qū)域,也是產(chǎn)生電勢差最大的區(qū)域,其他區(qū)域的面積相對來說比較小,只是A4區(qū)域面積的1/10左右。這樣可以在細化劃分區(qū)域的同時,保證時間復雜度不會過高,充分利用圓簡管道的特點。這種劃分方式可以讓管道內(nèi)壁的電極最大程度地讀取電勢值,通過區(qū)域權(quán)函數(shù)理論可以更詳細地反映流場內(nèi)的速度信息,提高仿真的精度。
根據(jù)式(2)的表達內(nèi)容,電極對間的感生電勢測量值為速度與權(quán)重函數(shù)和面積的乘積求和,因此,多電極電磁流量計測量公式可改寫成矩陣乘積的形式:
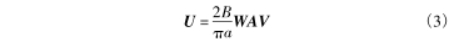
式中,W為ixj維度的區(qū)域權(quán)函數(shù)矩陣;V為包含i個區(qū)域軸向平均速度的速度向量;U為包含j個感應(yīng)電動勢測量值的電壓向量:A為ixi維以i個區(qū)域的面積為對角元素的對角陣。在本文的應(yīng)用中,i=j=7。
在實際應(yīng)用中,測得感應(yīng)電動勢后,多電極電磁流量計在對速度進行重構(gòu)以及得出流量的過程,從數(shù)學角度看其本質(zhì)是一個矩陣運算的過程。
矩陣A在完成區(qū)域劃分后,其面積大小為定值;并且電極所在坐標處的感應(yīng)電動勢可通過電極對測量出來,為因變量,因此矩陣U也已知;而區(qū)域權(quán)函數(shù)矩陣W是只與電磁流量計結(jié)構(gòu)有關(guān)的常數(shù)矩陣,通過COMSOLMultiphysics仿真可求得。
2基于有限元仿真的速度重構(gòu)
2.1區(qū)域電勢的有限元仿真
為獲得實驗所用電磁流量計的權(quán)函數(shù),首先根據(jù)實驗所用的流量計結(jié)構(gòu)進行仿真。
為了獲取橫截面電極上的仿真電勢值,可在模型開發(fā)器中選擇域點探針,并更新結(jié)果,即可在工作區(qū)探針表得到感應(yīng)電勢。在8個電極中把e1作為參考電.極,與其他7個電極構(gòu)成了7對電極組合,可以得到7x7共49個電壓測量值,如表1所示。
為提高權(quán)函數(shù)精度,管道內(nèi)流體速度可以適當提高,分別在區(qū)域A1~區(qū)域A7沿管道方向施加速度(洛倫茲項)500m/s,經(jīng)計算得到圖2所示的7張電勢分布圖,從左到右、上到下依次是區(qū)域A1~A7域A7,施加速度的電勢。.
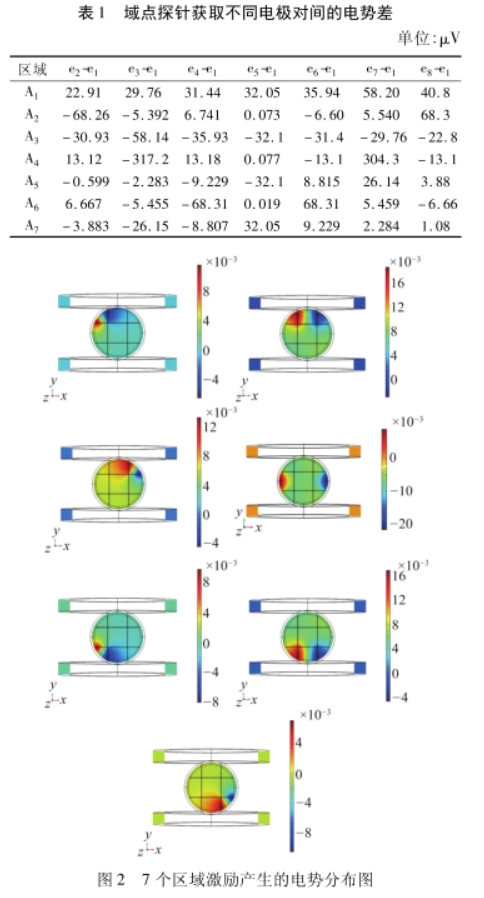
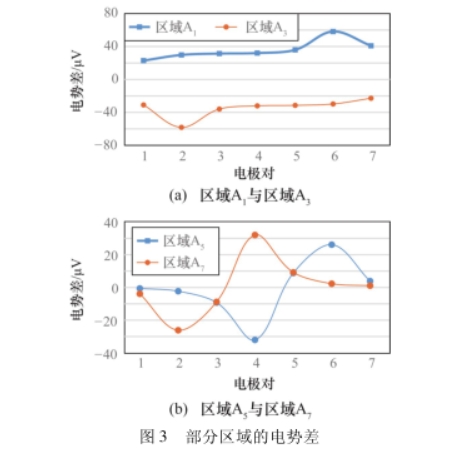
其中,部分區(qū)域的感應(yīng)電勢差的仿真如圖3所示,從圖3中的數(shù)據(jù)分布可以看出,由于仿真過程中所添加的速度分布的設(shè)置,仿真得到感應(yīng)電壓數(shù)據(jù)是以第
4對電極為對稱中心,同時區(qū)域劃分在測量面內(nèi)的分布也是對稱的。
通過傳感器得到感應(yīng)電勢差后,根據(jù)式(4)進行速度的重構(gòu):
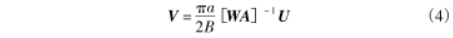
得出一維速度矩陣后,將區(qū)域速度乘以對應(yīng)區(qū)域面積即可得出流量信息。
2.2逆矩陣的求解
在經(jīng)典的數(shù)學物理學方程求定解問題中,問題的定解分為兩類,一類是適定問題,該類問題具有以下3個特性:①解是存在的;②解是唯--的;③解連續(xù)依
賴于初始值條件。而上述3個條件只要有一個不滿足就稱為不適定問題。
由于多電極電磁流量計中存在極化干擾、微分干擾等誤差,矩陣數(shù)據(jù)精度有限。如果采用對矩陣的精度要求較高的直接求逆法求逆矩陣,干擾與微小誤差會對速度結(jié)果造成較大的影響,所以使用直接求逆法得到的逆矩陣并不精確。
為了求得具有一定精度的穩(wěn)定近似解,數(shù)學物理.學中已經(jīng)提出許多有效的解法,其中一種就是正則化方法。其原理是通過對原不適定問題中的算子添加一個合適的擾動項,使之穩(wěn)定,從而解決逆問題的不適定性,使得產(chǎn)生的解是存在的[I@]。因此,采用選取吉洪諾夫正則化運算法則。在Matlab中,首先使用內(nèi)置的奇異值分解函數(shù)csvd獲得待求線性方程組的參數(shù)的奇異值[u,s,o];然后使用L曲線法l_curve(u,s,B)求得正則化參數(shù)lambda,最后使用吉洪諾夫正則化求解速度。求得的速度重構(gòu)值如圖4所示。
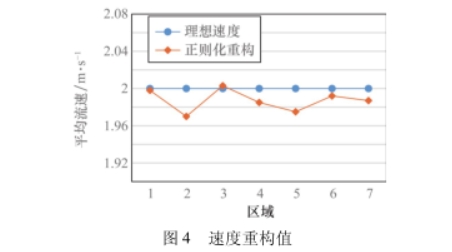
在設(shè)置為均勻流速的情況下,對感應(yīng)電勢差仿真數(shù)據(jù)進行正則化計算后的流速分布如圖4所示,從圖4中可以看出,仿真求得的速度重構(gòu)值精度較高,誤差在1.50%以內(nèi)。
3結(jié)束語
本文基于電磁感應(yīng)原理與權(quán)函數(shù)理論,為電磁傳感器設(shè)計了一種8電極的多電極電磁流量計。在COMSOLMultiphysics軟件.上完成了勵磁線圈、圓簡形管道、洛倫茲力的設(shè)計與仿真,并使用Matlab軟件對速度重構(gòu)矩陣進行求解。結(jié)果證明:7塊區(qū)域的劃分與正則化求解保證了系統(tǒng)在環(huán)境變化時的魯棒性與正確率。重構(gòu)后的速度與理想速度的精度在±1.50%,可以較好地實現(xiàn)圓簡形電磁流量計的速度復原。
本文來源于網(wǎng)絡(luò),如有侵權(quán)聯(lián)系即刪除!



