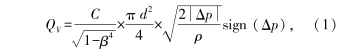摘要:為了研究孔板流量計在動態非穩定流態或振蕩流態下的瞬時壓力-流量特性,理論分析了孔板前后的旋渦城大小隨流速變化是引起孔板進出口瞬時流量差的主要原因.借助CFD數值解析方法,建立孔板模型,并在模型入口加載某一頻率下的正弦流速,對孔板流量計在振蕩流態下的瞬時壓力-流量特性進行分析.結果表明:當孔板流量計處于低頻振蕩流動狀態時,孔板兩端差壓也處于周期振蕩狀態,差壓與節流孔瞬時流量同頻不同相,差壓幅值隨入口流速振幅增大而線性增大,且線性增長系數與振蕩頻率相關;孔板的入口與出口存在周期波動的瞬時流量差,振蕩頻率越大或入口流速峰值越小,瞬時流量差的波動越小,由于相位滯后和瞬時流量差的存在,使孔板流量計的測量流量與實際出口流量之間存在偏差.振蕩頻率越大,偏差也越大.
孔板流量計因其結構簡單、耐用而成為目前國際上標準化程度最高、應用最為廣泛的一種流量計,因此研究節流孔的流量特性,對提高孔板流量計測量不確定度的認識具有很重要的意義.孔板流量計通過測量壓差進而獲得流量.當液流經過節流孔,流束縮小,流速變大并伴隨著較大的壓力降.流束的最小橫斷面出現在實際縮口的下游,稱為縮流斷面.在縮流斷面處,壓力最低.壓降的產生是由于在孔板的兩側側面出現回流區及旋渦域,造成較大的內部紊流和能量損耗的結果[1-2].旋渦域的大小取決于流動雷諾數,隨著雷諾數的增大,渦旋強度增加[3].
流體力學中對孔口恒定出流的描述為孔板結構的設計提供了理論依據.但實際應用中,由于外界激勵引起的壓力波動,圓管內流體常處于動態非穩定流態或振蕩流態[4],孔板流量計內部流場結構變化極為復雜,因此,計量孔板的瞬時流量特性往往與理論分析結果存在偏差因此,有必要對孔板在非穩定流態下的流量特性進行研究.
通過Fluent流體仿真程序,對不同節流孔直徑比的孔板,以水為介質在振蕩流態下的流動過程進行仿真,對其瞬時壓力-流量特性進行分析.
1理論分析
通常在特定測壓位置和特定流體參數情況下,根據流體流動的連續性方程和伯努利方程可推導出孔板前后差壓△p與流經節流孔的體積流量QY滿足以下函數關系[5],即
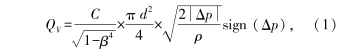
式中:C為流出系數;ρ為流體密度;β為節流孔的直徑比(β為節流孔直徑d與圓管內徑D的比值,即β=d/D);sign為符號函數*.
圓管進口流量可計算公式為
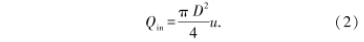
孔板流量計通過測量節流孔兩端差壓進而獲得節流孔流量QV.對于不可壓縮的定常流,圓管進口流量Qin和出口流量Qout與節流孔流量QY相等,聯立以上方程可得節流孔兩端差壓與人口流速的關系表達式為

由式(3)可知,孔板兩端差壓也呈周期性波動,.其振蕩頻率與孔板人口流速振蕩頻率相同.
孔板前后存在旋渦域.旋渦域的大小占據圓管空間,液體在旋渦域停留,不流向下游管道.旋渦域增大,則流向圓管出口的液流減少.由于孔板前后游渦旋強度隨流動雷諾數增大而增大,即隨流速增加旋渦域變大3],.在振蕩流態下,旋渦域大小隨入口流速變化也表現為周期性變化狀態,變化頻率與流速振蕩頻率相同.因此,在某一極短時間段內,旋渦域的體積變化量表現為圓管進、出口的瞬時流量之差.對于不可壓縮的非定常流,人口瞬時流量Qin與出口瞬時流量Qout和節流孔瞬時流量QY滿足以下關系,即

式中:△Q表示圓管進出口瞬時流量差.瞬時流量差的存在,使孔板流量計實際測量流量Qv與出口瞬時流量Qout之間不可避免存在偏差.
事實上,由于節流孔的壓降作用,當孔板下游壓力低于液體飽和蒸氣壓以下,氣泡將在下游管道產生,形成閃蒸現象.當壓力上升,氣泡破裂瞬間產生局部空穴,高壓液體重新流向這些空間.顯然,氣泡和空穴占據了下游管道空間,使進、出口流
量Qm與Qout,存在差異,出現瞬時流量差實際孔板流量計使用過程中避免閃蒸和空穴現象的出現,故文中對其影響不做表述.
為進一步探究孔板的瞬時壓力流量特性,文中以上述理論分析為基礎,結合有限元分析思想,對孔板流量計在低頻微幅振蕩流態下的壓力流量特性進行了分析.
2期修仿真
2.1控基文圖
文中選用RNGk-ε湍流模型對孔板的流量特性進行模擬.該模型的控制方程分別為連續性方程

上述式中:xi,xj分別為縱向和橫向坐標;ui,uj分別為縱向和想象的速度分量;p為流體壓力;v為流體運動黏度;vt為流體渦流黏度,vt=Cμk²/Ɛ,其中k為湍動能,Ɛ為湍動耗散率,Cμ=0.085.
模型邊界條件包括速度人口、壓力出口、無滑移壁面邊界,在近壁面區域采用標準壁面麗數進行處理.采用軸對稱邊界,即模型對稱軸的徑向速度為0.在求解離散方程組和壓力速度耦合時選擇了SIM-PLE算法,動量和湍流動能分別采用的是二階迎風與一階迎風差分格式.
2.2仿真文收
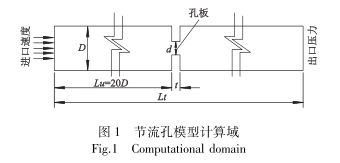
利用孔板模型的軸對稱性的特征,在圓柱坐標系下建立它們的1/2實體模型,取壓方式采用D-D/2取壓其計算域如圖1所示.孔板.上游直管段長度為20D,充足的上游管長能夠確保液流在孔板上游為充分發展的湍流流動.模型具體尺寸,其中D=12.3mm,β=0.247,Lu=246mm,Lt=494mm,t=2mm.
為了表現孔板前后的流場變化情況,首先在壁面附近劃分邊界層網格,邊界層第一次厚度為0.1mm,共10層,高度增長因子1.1.其次,為了提高孔板附近的計算精度,對靠近孔板部分的網格進行局部加密,離節流孔越遠,網格越稀疏最后,利用結構化網格生成方式劃分其余部分網格.
文中所選用的流體介質為常溫狀態下的水.人口流速設定為某一-頻率下的正弦流動u=uarg+uamp·sin(2πƒt),選擇不同平均流速uarg、流速振幅uamp和振蕩頻率ƒ參數作為節流孔的人口流速,具體參數見表1.利用UDF功能將該自定義速度函數加載在模型的速度人口.
3網出第日
3.1振蕩差絡
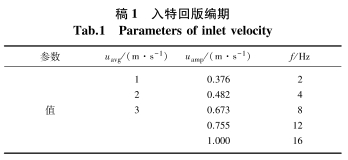
通過后處理后可以觀察到,當人口流速為某一頻率下的正弦流動時,孔板兩端將出現與人口流速頻率相同的振蕩差壓.如圖2所示,節流孔瞬時流量與差壓振蕩頻率相等且具有固定的相位滯后.相位滯后意味著測量壓差不能反映當時的流量情況.此外,由于壓差測量裝置的動作時限,測量壓差滯后,不能及時反映瞬時壓差的變化因此,在振蕩流態下,孔板流量計對瞬時流量的測量存在不確定性.
圖3為人口流速振幅與差壓幅值的關系.對于同一振蕩頻率的入口流速,孔板兩端差壓幅值隨人口流速振幅增大而線性增大,但其線性增長系數與振蕩頻率有關.
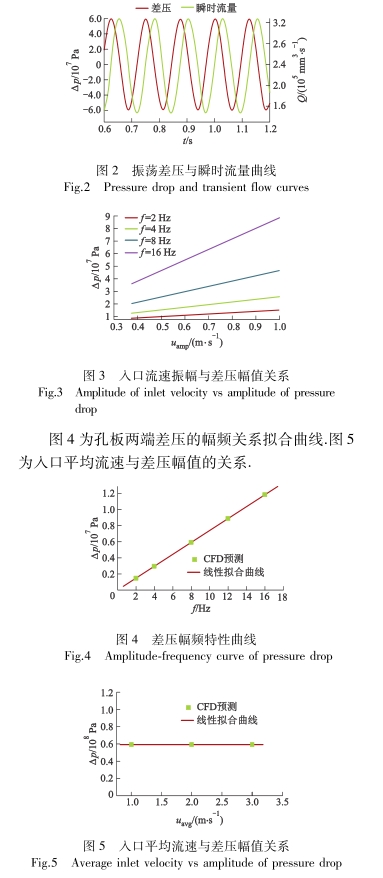
從圖4中可以看出當人口流速振幅一定時,節流孔兩端差壓的振蕩幅值隨振蕩頻率的增大而增大.差壓幅值與振蕩頻率存在近似一次線性關系.
在孔口恒定出流情況下,測量流量與實際節流孔流量Qv相同.而在振蕩流態下,差壓幅值隨振蕩頻率線性增大,則測量流量幅值越大,與實際節流孔流量的偏差也越大.
從圖5中可以看出,平均入口流速的變化,對壓力幅值的影響幾乎可以忽略.
3.2瞬時流量差
在振蕩流態下,孔板前后回流區和旋渦域的大小隨人口流速變化不斷改變,導致進出口流量存在.瞬時流量差△Q,如圖6所示.瞬時流量差表現為復雜的周期性波動,其波動周期與差壓振蕩周期相同,相位介于瞬時流量和差壓兩者之間,且稍滯后于振蕩差壓.當差壓增大至峰值點時,瞬時流量差趨向其波峰,并在到達峰值點后反向階躍.
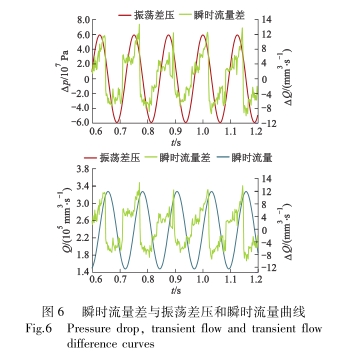
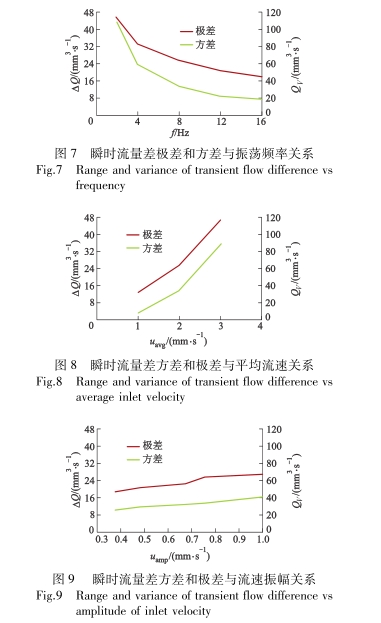
為研究人口流速各參數對瞬時流量差的波動特性影響,對仿真記錄的瞬時流量差數據作方差分析和極差分析,以此描述瞬時流量差的波動情況.瞬時流量差的極差和方差與振蕩頻率關系如圖7所示.當入口平均流速和流速振幅不變時,瞬時流量差的極差和方差隨人口流速的振蕩頻率增大而減小也即人口流速頻率越大,瞬時流量差的波動程度越小,同時波動的峰值也越小.
圖8為入口平均流速與瞬時流量方差及極差的關系.當振蕩頻率和流速振幅相同時,人口平均流速越大,瞬時流量差的方差和極差越大.圖9為瞬時流量差方差和極差與流速振幅關系.從圖中可以看出,當人口平均流速相同時,對于給定的振蕩頻率,瞬時流量差的方差和極差隨著流速振幅增大而增大.因此,當人口流速峰值越大,瞬時流量差波動也越大,瞬時流量差就越不穩定.
4結論
當孔板流量計所計量不可壓縮流體為低頻振蕩流動狀態時,通過前述CFD分析,得到如下結論:
1)孔板兩端差壓為周期振蕩狀態,差壓與節流孔瞬時流量同頻不同相.差壓幅值隨人口流速振幅增大而線性增大,且線性增長系數與振蕩頻率相關.
2)圓管人口與出口存在周期波動的瞬時流量差,振蕩頻率越大或人口流速峰值越小,則瞬時流量差的波動也越小
3)在振蕩流態下,由于相位滯后和瞬時流量差的存在,使孔板流量計的測量流量與實際出口流量之間存在偏差振蕩頻率越大,偏差也越大..
4)孔板流量計作為的流量計量的常用元件,該分析結果對孔板的結構設計及系統的整體動態特性研究具有重要意義. 本文來源于網絡,如有侵權聯系即刪除!