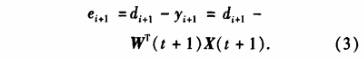摘要:研究了獲取管道振動噪聲干擾特征的方法,介紹了基于加速度傳感器的管道振動信號的采集.結合渦街流量信號和管道振動信號的頻譜分析結果,指出了管道振動信號頻率與渦街流量計信號的主要干擾分量頻率直接相關.研究表明,可通過獲取管道振動加速度信號特征,來間接獲得渦街流量信號中主要噪聲的頻率特征.基于這一研究結論,以管道振動信號的特征信息為參考輸人,驗證了通過自適應濾波對渦街流量信號中振動噪聲的濾波方法.
現今渦街流量計的使用越來越廣泛,因其屬于流體振動型流量計,故對振動干擾顯得非常敏感.振動干擾是影響渦街測量的主要干擾之-“,國內外的學者和公司對渦街流量計抗振動問題進行了大量的研究21,其中以Rosemount公司的8800A'31和F+P公司的VT/VR型為代表[4].
本研究從獲取管道振動噪聲干擾特征的方法著手,分析得出了管道振動信號頻率與渦街流量信號的主要干擾分量頻率直接相關,研究了一種基于加速度傳感器的管道振動信號采集和對應的自適應濾波方法.
1機械管道振動對渦街流量計信號的影響
表1是不同流體傳感器對過程干擾的敏感性影響程度的統計[5].表中“++”表示高敏感(讀數誤差10%或更高),"+”表示敏感(讀數誤差1%),表示不敏感(讀數誤差小于1%)

從表1中可以得知,渦街流量測量中干擾影響大的成分為機械管道振動干擾和周期性的低頻脈動干擾.
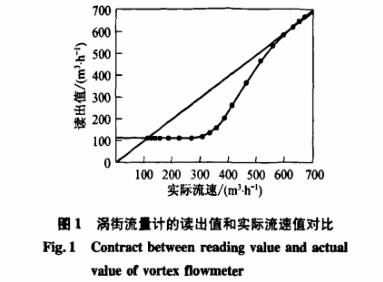
討論了在加速度為1g,垂直振動頻率為100Hz的振動于擾對渦街流量計信號輸出的影響,如圖1所示在沒有流速的情況下,渦街傳感器檢測到管道振動,并錯誤判斷100Hz是流量信號,因此錯誤地顯示了120m'/h的流速.
2渦街流量信號與管道振動信號特征聯系的試驗分析
振動干擾是主要的干擾成分之一.若要將各信號成分特征一--進行分離,目前常用及成熟的方法就是頻譜分析[78].在離線頻譜分析中,可以依據人腦的判斷來有效地區別振動噪聲和渦街信號的頻率、能量分布的不同.然而在實際工程應用中,若噪聲能量大于信號能量,則在線的頻譜分析雖然可以分辨出能量的峰值,但無法有效區分能量的峰值是信號的還是干擾的,因此可能會跟蹤了錯誤的振動干擾噪聲..
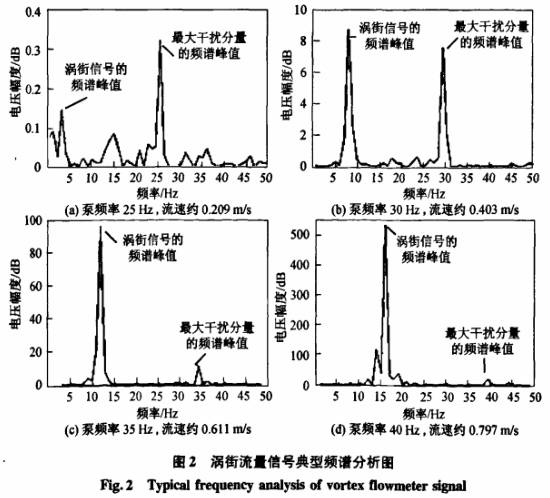
本研究對不同流速和泵頻率組合下的渦街流量信號進行了數據采集和頻譜分析,其中水泵采用格蘭富AP12.40單級潛水泵,分別調節流速約0.209,0.403,0.611,0.797m/s.控制水流速的大小,在每一開度下,再分別設置水泵工作頻率為25,30,35,40Hz,以輸人不同的振動干擾信號,如圖2所示.可見當流速小時噪聲能量接近甚至大于實際信號能量,在線的頻譜分析很難判斷..
考慮到管道的振動是振動干擾直接的物理響應,當手觸摸管道時,明顯可以覺察到管道有規律地振顫.基于以上分析,結合振動測量知識,本研究認為可以嘗試引人加速度傳感器來采集管道振動的信號[910.
試驗中,加速度傳感器的選取較為重要.本研究加速度傳感器試驗選擇了美國ADI公司的ADXL202,這是-種低成本、低功耗、功能完普的雙軸加速度傳感器,其測量范圍為+2g.
本試驗使用A/D數據采集卡,將ADXL202的模擬輸出信號轉換為數字信號送人PC機進行處理,基于Labwindows/cvi測控平臺的PC機能夠方便地實現數據采集.
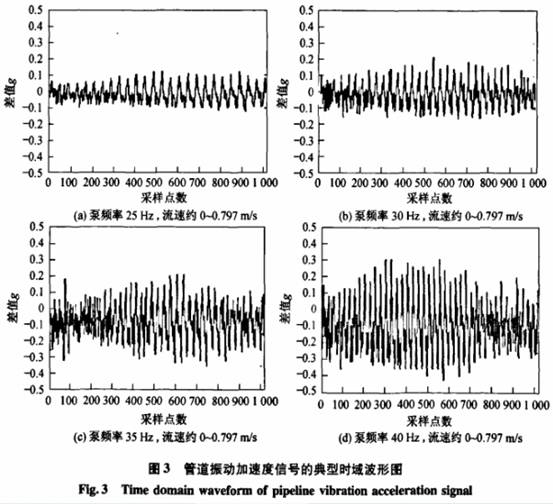
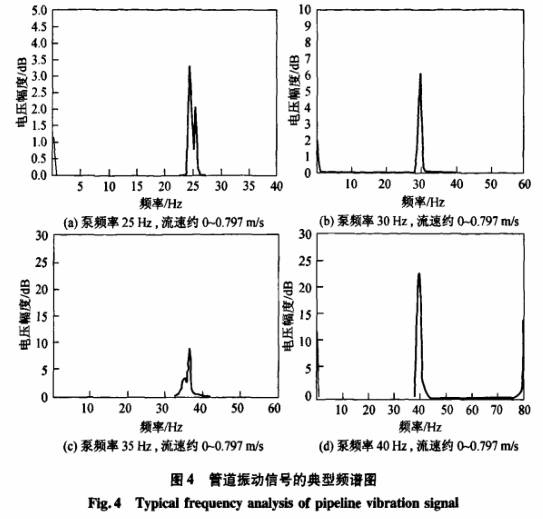
試驗工作狀態:分別調節流速約為0,0.209,0.403,0.611,0.797m/s,控制水流速的大小,并在每--開度下,再分別設置水泵工作頻率為25,30,35,40Hz.加速度傳感器的模擬輸出信號輸人到PC機的A/D采集卡,采樣頻率1000Hz.對不同流速和泵頻率組合下的管道振動信號進行數據采集和頻譜分析.圖3為所有組合下,采樣得到的管道振動加速度信號的典型時域波形圖.圖中橫坐標為采樣的點數,共1024點;縱坐標為相對于Og標定值的差值,縱坐標基準值0對應了0g的標定值.圖4所示為對應的管道振動信號的典型頻譜圖.
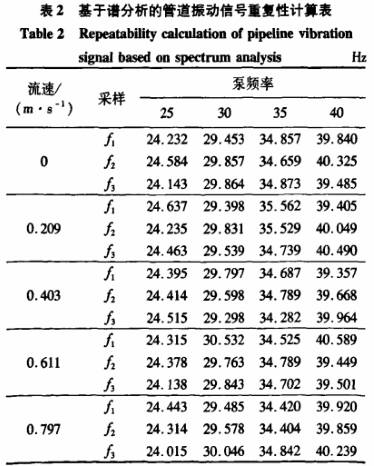
為了驗證所采集振動信號是否具有重復性,本研究對每種工況下組合的管道振動信號分別進行了3次重復采樣,每次1024點,采樣頻率1000Hz.表2是各次數據分析得到的頻率值.
由表2的數據可以看出,管道振動的數據頻譜分析得到的振動頻率值重復性很高.
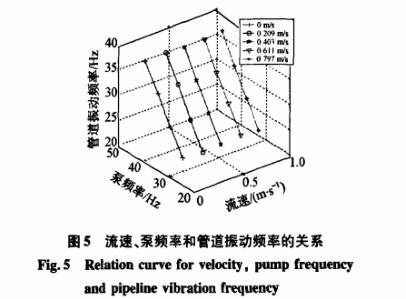
對表2的重復性數據計算平均值,并由平均值畫出了流速、泵頻率和管道振動頻率的關系曲線,如圖5所示.分析結果表明,不論試驗裝置工況如何,管道振動信號的頻率和能量只與泵工作頻率相關,泵頻率越大,則振動信號的頻率和能量越大.
3對管道振動自適應濾波的試驗
通過以上分析可以得出結論,水泵工作引起的管道振動干擾直接耦合到了渦街輸出信號中.試驗數據顯示,在各種流動狀態下,渦街信號中迭加的千擾頻率與管道加速度振動頻率近乎于相等,且與試驗用的水泵工作頻率相近.
通過加速度傳感器獲得有效的管道振動頻率后,可以將之等同為渦街流量信號中主要干擾信號的頻率.本研究提出以管道振動信號的特征輸人為參考信號,采用自適應小均方誤差(LMS)數字濾波器方法,來對渦街流量信號振動干擾進行處理11.LMS濾波器輸出為
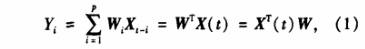
式中,W為濾波器各系數組成的向量,X為監測值組成的向量.
LMS算法的基本思想是利用優化方法中的速下降法.根據推導,可得權系數的迭代公式為
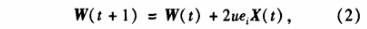
式中,u為自適應系數,取值大小影響到收斂速度、估計值的方差和算法的穩定性.誤差e;的迭代計算公式為
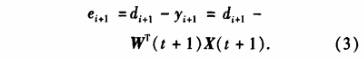
用式(2)更新權系數W(t+1),隨著新數據不斷輸人,不斷重復使用式(2)和式(3)進行迭代,使W逐漸趨近于W。.
設采集獲得的渦街流量信號為原始信號,參考輸人為采集獲得的管道振動加速度信號,濾波器系統如圖6所示.
由上述自適應濾波器的算法,可得到系數W;的計算值為
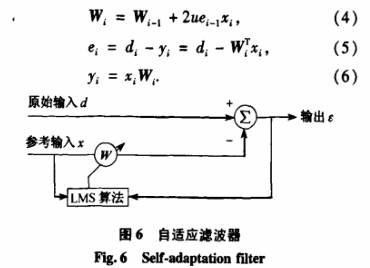
設定u值,通過式(4)~(6)的循環迭代,使W;逐漸趨近于W.
如前所述,u為控制LMS算法收斂速度和穩定性的系數,u值過大可能導致發散,過小又可能使收斂速度變慢.本研究通過大量的計算,不斷修正和比較,使其接近佳值.通過試驗計算,確定u=0.1.
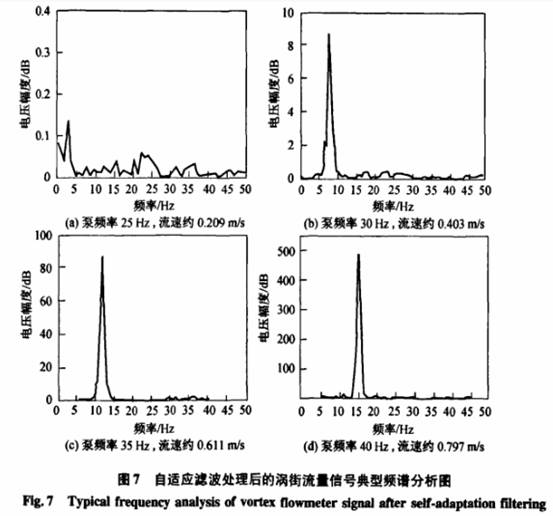
圖7為濾波后的信號頻域圖.從圖中可以看出,主要的管道振動干擾已經被消除,濾波后的信號信噪比提高很多..
4結束語
本研究是在自有試驗裝置上對一部分渦街傳感器進行試驗的.盡管不同的管道振動有其特殊性,但管道振動問題也有一-定的普遍性.本研究通過基于加速度傳感器的管道振動信號的采集和頻譜分析,指出了管道振動信號頻率與渦街流量信號的主要干擾分量頻率直接相關.并采用自適應濾波方法,驗證了對渦街流量計振動噪聲濾波的有效性,為消除振動噪聲提供了一種有效的途徑值得注意的是,本研究主要針對解決以泵的干擾為主的管道振動噪聲問題,對于解決其他有一定規律的管道振動噪聲也有適用性.本研究中加速度傳感器的安裝位置至關重要,會影響振動信號的檢測以及對渦街信號濾波處理的結果.
以上內容源于網絡,如有侵權聯系即刪除!