摘要:采用有限元方法,針對三對多電極電磁流量計電極在不同位置時權重函數(shù)分布情況進行數(shù)值仿真。提出2個描述權重函數(shù)分布均勻度的指標:最大偏差和整體均勻度,并在電極數(shù)目和位置不同情況下對權重函數(shù)的分布情況進行分析比較。結果表明,電磁流量計權重函數(shù)分布不僅與電極數(shù)目有關,還與電極所在的位置有關。通過合理設計電極位置,三對電極電磁流量計在權重函數(shù)分布均勻度和平均強度兩方面都優(yōu)于單電極對電磁流量計。.
1引言
電磁流量計是一種用于導電性液體流量測量的儀表o由于其不受溫度、壓力、流體密度和粘度等因素影響,且其內(nèi)部光滑無阻流部件[3],不會對流體產(chǎn)生阻力從而導致壓力損失,因此在工業(yè)生產(chǎn)過程的流量測量中得到廣泛應用。權重函數(shù)表示管道橫截面上不同位置流速對流量計輸出信號的貢獻大小,權重函數(shù)均勻則各點流速貢獻相同。所以,在電磁流量計的設計中,總是希望權重函數(shù)分布越均勻越好。對外流式電磁流量計和油管之間環(huán)形區(qū)域的權重函數(shù)分布情況進行了理論推導和仿真。管道橫截面上流體速度呈非軸對稱分布時,采用傳統(tǒng)單電極對電磁流量計會產(chǎn)生較大的測量誤差。而多電極電磁流量計可以從多角度多位置測量感應電動勢,故可用于非軸對稱管流流量的精確測量。
目前,對多電極電磁流量計權重函數(shù)分布情況的還較少。本文多電極電磁流量計在管道橫截面上權重函數(shù)的分布特性。結果可為多電極電磁流量計傳感器的結構優(yōu)化提供進--步的基礎。
2基本方程與權重函數(shù)
當導電性液體在磁場中作切割磁力線運動時,液體中有感應電流產(chǎn)生。根據(jù)歐姆定律有:

對均勻磁場型電磁流量計,為便于分析和闡明其物理意義,通常使用“長筒流量計”物理模型[13]如圖1所示,設磁場區(qū)域長度和電極長度均為2L,此時電極呈線狀。當L-→∞時,方程的求解就可由三維空間坐標問題簡化成=維平面坐標問題。
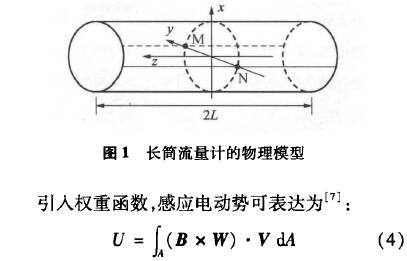
式中:A為測量管容積,W為權重函數(shù),W=▽G,G為格林函數(shù)。W是三維空間函數(shù),Wx、Wy、Ws分別為W在坐標軸x、y、z方向,上分量,對長簡流量計只考慮y方向上分量Wy。假設磁場方向平行于x軸,流速平行于z軸,則B=Bx,V=Vz。由以上條件,可得:
(B×W)·V=BWyV(5)
由式(5)可知,電極兩端產(chǎn)生的感應電動勢不僅與流速有關,還與權重函數(shù)分布有關。
3權重函數(shù)的仿真與分析
3.1單電極對電磁流量計權重函數(shù)數(shù)值仿真
根據(jù)格林函數(shù)性質(zhì)和電磁流量計邊界條件,可得長筒流量計權重函數(shù)解析式[7]:

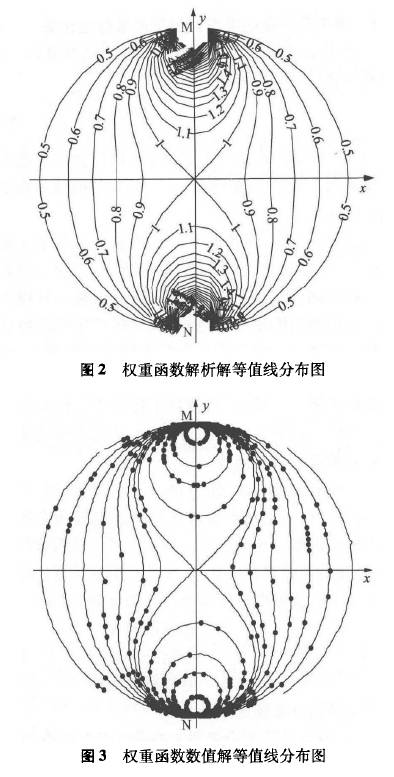
式中r為管道內(nèi)半徑。由式(6)可得管道內(nèi)電極所在橫截面上W的分布情況,r=1時其等值線分布如圖2所示。
由圖2可知,在管道中心處W值為1,沿著y軸.向電極M、N處移動時,W值逐漸增大;沿著x軸向管壁移動時,W值逐漸減小至0.5。權重函數(shù)越大的區(qū)域內(nèi)的流體速度對電極M、N所產(chǎn)生感應電動勢的貢獻越大。由權重函數(shù)分布規(guī)律可以看出,整個測量區(qū)域內(nèi)的流體速度對電極所產(chǎn)生感應電動勢的影響程度不一樣,這就解釋了傳統(tǒng)單電極對電磁流量計對流速分布的敏感性,導致其無法準確測得非軸對稱流的平均流速。
采用有限元方法,使用Malab軟件中PDE工具.箱,對單電極對電磁流量計在管道內(nèi)電極所在橫截面上權重函數(shù)分布情況進行數(shù)值仿真。在數(shù)值仿真時,關鍵是求解格林函數(shù)G,由于C滿足拉普拉斯方程▽2G=0,假設電磁流量計邊界條件如下:

(4)對求解區(qū)域網(wǎng)格化,網(wǎng)格劃分越細,精度越高,但計算量會增大;
(5)求解橢圓型偏微分方程可得u,即G;
(6)求解格林函數(shù)G在y方向上的梯度,即Wy;
(7)畫出Wy的等值線分布圖。
如圖3所示,為權重函數(shù)數(shù)值解等值線。將其與圖2進行對比,發(fā)現(xiàn)二者沒有太大差別。表明利用有限元方法計算權重函數(shù)是高效可行的方法,并且可通過增加網(wǎng)格密度來提高計算精度。
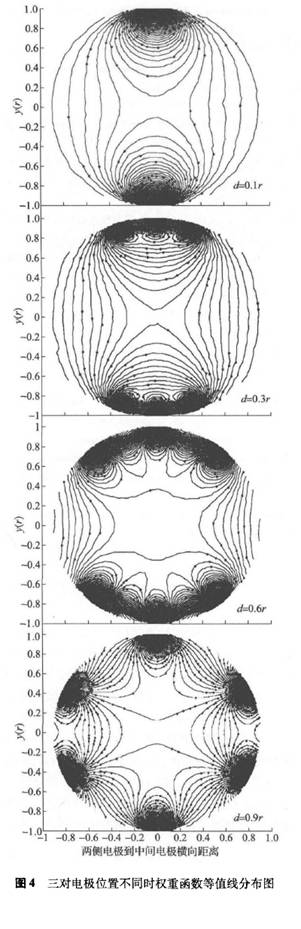
3.2三對電極電磁流量計權重函數(shù)數(shù)值仿真
針對三對電極電磁流量計,對電極處于管道橫截面上不同位置時權重函數(shù)的分布情況分別進行仿真,結果如圖4所示。三對電極的位置分布如下:中間一對電極橫坐標為x=0,兩側電極關于中間電極對稱,它們到中間電極的橫向距離為d,d的范圍為0.1r~0.9r,其中r為傳感器管道內(nèi)半徑。
3.3權重函數(shù)的數(shù)值分析
定義:對管道橫截面上權重函數(shù)分布進行數(shù)值仿真時,設求解區(qū)域被劃分成n個網(wǎng)格,第k個網(wǎng)格對應的權重函數(shù)值為Wk(k=1,2,.,n),則權重函數(shù)W的最大偏差RM可表示為:RM=MAX

應區(qū)域內(nèi)權重函數(shù)的最大偏差程度;RD則反應了區(qū)域內(nèi)權重函數(shù)分布的整體均勻程度,RD值越小,權重函數(shù)分布的整體均勻程度越理想。
依據(jù)上面兩個指標,計算電極處于不同位置時權重函數(shù)分布均勻度,如表1所示。從圖4和表1可知,權重函數(shù)分布情況不僅與電極數(shù)目有關,還與電極分布的位置有關;隨著兩側電極與中間電極距離增大,權重函數(shù)的平均值W0逐漸減小,即相同流速對流量計輸出信號的貢獻逐漸減弱;隨著兩側電極與中間電極距離增大,權重函數(shù)的最大偏差Rm和RD的值都逐漸增大,權重函數(shù)的整體均勻度逐漸降低。
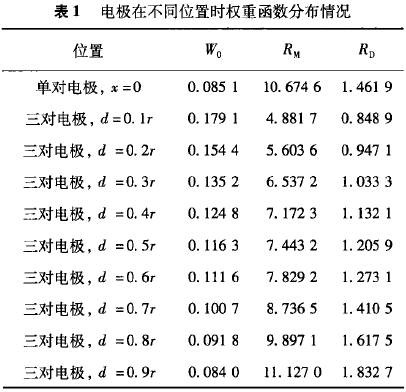
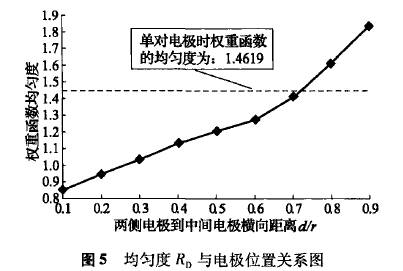
權重函數(shù)均勻度Rp隨電極位置變化趨勢如圖5所示。從表1和圖5可知,對于三對電極電磁流量計,當中間一對電極橫坐標為x=0,兩側電極到中間電極的橫向距離d≤0.7r時,整體均勻度Rp<1.4619,最大偏差RM<10.6746,即三對電極電磁流量計比傳統(tǒng)單電極對電磁流量計權重函數(shù)分布的更為均勻,其管道橫截面.上不同位置流體速度對流量計輸出信號的貢獻更趨向-致,表明三對電極電磁流量計對流速分布的敏感性減弱;權重函數(shù)平均值W0>0.0851,表明相比單電極對電磁流量計,管道橫截面上相同流速對流量計輸出信號的貢獻增強,即在相同條件下,三對電極電磁流量計可獲得更強的感應電動勢信號。
以上針對三對電極電磁流量計權重函數(shù)分布隨電極位置變化情況進行了仿真分析,結果為多電極電磁流量計的結構優(yōu)化提供了參考依據(jù),具有-定的理論指導意義。雖然從理論上電極數(shù)目越多,流體平均速度的測量精度越高,但從實際制作、成本和可靠性來講,電極數(shù)目不可能無限增多,而且電極數(shù)目的增加會延長數(shù)據(jù)采集時間,導致系統(tǒng)實時性降低,通常只要測量精度達到要求就可以了。當然對精度有特殊要求時,可相應增加或減少電極數(shù)目。
4結論
采用有限元方法對傳統(tǒng)單電極對電磁流量計權重函數(shù)分布進行了數(shù)值仿真,將仿真結果與已有權重函數(shù)解析解作對比分析,驗證了有限元方法求解權重函數(shù)的可行性和有效性;針對三對電極電磁流量計,電極在不同位置時,對電極所在橫截面上權重函數(shù)分布情況分別進行數(shù)值仿真;定義了兩個描述權重函數(shù)分布均勻度的指標:最大偏差和整體均勻度。依據(jù)這兩個指標,在電極數(shù)目和位置不同情況下,分別對權重函數(shù)進行仿真分析。結果表明通過合理設計電極位置,三電極對電磁流量計在權重函數(shù)分布均勻度和平均強度兩方面都優(yōu)于單電極對電磁流量計。
以上內(nèi)容源于網(wǎng)絡,如有侵權聯(lián)系即刪除!








