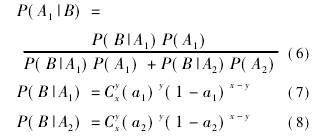摘要:分析
渦輪流量計產生機械慢表的原因,依據數據傳輸系統傳回的停機延時流量制訂機械慢表的評估方法,,當流量計停機延時流量評估得分小于等于20分時,通過貝葉斯定理判斷,依據評估得分發現該流量計為機械慢表的正確率的大于等于90%的可信度為94.94%。如果客戶用氣設備每天至少停機1次,則評估周期最多需要30d,該評估方法可將故障發現周期從2a縮短到30d,最大程度降低燃氣公司的機械慢表損失。
1概述
在日常工作中,渦輪流量計因軸承卡死等機械故障而造成的流量計不計量現象(俗稱機械死表),通常都能被燃氣公司工作人員及時發現,追繳氣量也較容易。而因軸承磨損導致的計量誤差偏大的現象(俗稱機械慢表),由于現場缺乏有效手段,較難及時發現,目前診斷機械慢表只有定期將流量計通過檢測臺,用音速噴嘴等標準計量裝置檢定,即流量計周檢。根據JJG1037—2008《渦輪流量計檢定規程》(以下簡稱JJG1037—2008)要求,渦輪流量計檢定周期為2a,即出現機械慢表時,在及時進行流量計周檢的情況下,該故障最長可能存在2a。
2形成機械慢表的原因分析
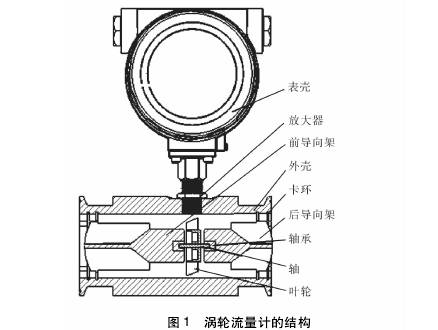
渦輪流量計的主要計量部件為機芯,渦輪流量計的結構見圖1。
渦輪流量計機芯由軸、軸承、葉輪組成,機芯的葉輪兩端由軸承支撐,當流體通過時,沖擊葉輪,對葉輪產生驅動力矩Mτ,使葉輪克服機械摩擦力矩Mτm、流體阻力矩Mτf以及磁電轉換器對葉輪產生的電磁反作用力矩Mτe而產生旋轉。由此可以建立葉輪的運動微分方程:
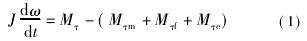
式中
J———葉輪的轉動慣量,kg·m2
ω———葉輪的旋轉角速度,rad/s
t———時間,s
Mτ———氣體流動對葉輪所產生的驅動力矩,N·m
Mτm———葉輪旋轉所產生的機械摩擦力矩,N·m
Mτf———流體阻力矩,N·m
Mτe———電磁反作用力矩,N·m
式(1)中通常電磁反作用力矩Mτe比較小,可以忽略。正常工作條件下,可認為管道內流量不隨時間變化,即葉輪以穩定的角速度旋轉。即存在

由于機芯的軸與軸承直接接觸,在氣體中的粉塵、雜質等作用下,葉輪旋轉就必然導致軸與軸承之間產生摩擦,進而產生磨損,工作時間越長,工況環境越差,潤滑越不利,磨損也就越嚴重,從而機械摩擦力矩Mτm越來越大[1]。使用初期,葉輪以應有角速度旋轉,如果機械摩擦力矩越來越大,葉輪的旋轉角速度會小于應有角速度,雖然隨著角速度的降低,流體阻力矩變小,但是由于機械摩擦力矩增大,仍達到了穩定工況。這種葉輪旋轉角速度變小的現象,叫流量計計量偏慢現象(即機械慢表)。因此認為:機械摩擦力矩Mτm增大是造成渦輪流量計機械慢表的主要原因。
3流量計工況數據分析
隨著通信技術不斷發展,燃氣遠傳數據傳輸系統已逐步被燃氣公司采用,該系統現場通過有線通信采集各項數據,再通過無線GPRS每2min一次上傳數據至服務器,可隨時了解燃氣溫度、燃氣壓力、瞬時流量、累積流量等實時信息,主要應用于計量管理、抄收、預付費管理等方面[2]。
①渦輪流量計葉輪慣性旋轉時間
當用氣設備停止用氣時,管道內氣體停止流動,葉輪由于慣性還在旋轉,此時流量計仍有逐漸下降的瞬時流量顯示。根據GB/T21391—2008《用氣體渦輪流量計測量天然氣流量》附錄C的相關解釋,在用氣設備停機后,流量計葉輪旋轉時間是評估該儀表運行工況的重要參數。
測量常用的3種型號新流量計在用氣設備停機后葉輪的慣性旋轉時間,為了確保數據準確,設備停機時的流量負荷選定在流量計量程的10%~90%,流量計葉輪慣性旋轉時間實驗結果見表1。
表1流量計葉輪慣性旋轉時間實驗結果
| 流量計型號 |
用氣設備停機時瞬時流量占流量計最大量程的占比/% |
測量次數/次 |
用氣設備停機后葉輪平均慣性旋轉時間/s |
LWQZ-50Z |
10 |
10 |
142 |
LWQZ-50Z |
20 |
10 |
145 |
LWQZ-50Z |
40 |
10 |
152 |
LWQZ-50Z |
50 |
10 |
150 |
LWQZ-50Z |
60 |
10 |
154 |
LWQZ-50Z |
90 |
10 |
155 |
LWQZ-80Z |
10 |
10 |
171 |
LWQZ-80Z |
20 |
10 |
172 |
LWQZ-80Z |
40 |
10 |
175 |
LWQZ-80Z |
50 |
10 |
177 |
LWQZ-80Z |
60 |
10 |
179 |
LWQZ-80Z |
90 |
10 |
183 |
LWQZ-100Z |
10 |
10 |
190 |
LWQZ-100Z |
20 |
10 |
197 |
LWQZ-100Z |
40 |
10 |
201 |
LWQZ-100Z |
50 |
10 |
205 |
LWQZ-100Z |
60 |
10 |
209 |
LWQZ-100Z |
90 |
10 |
212 |
由表1可以看出,當停止用氣后,流量計葉輪平均慣性旋轉時間均大于140s,而根據前文分析可知,當流量計為機械慢表時,機械摩擦力矩Mτm增大,葉輪的旋轉角速度ω急速下降,用氣設備停機后葉輪慣性旋轉時間縮短。因此,停機后慣性旋轉時間是關鍵切入點。
②停機延時流量
由于計量正確的渦輪流量計葉輪在用氣設備停機后葉輪平均慣性旋轉時間均大于140s,對所監控的流量計停機時連續運行數據進行分析,得出計量正確的流量計在用氣設備停機后仍會有小流量數據傳輸,將該流量定義為停機延時流量。某加氣站計量正確的流量計用氣設備停用時連續數據記錄見表2。瞬時工況流量為1.90m3/h的流量為停機延時流量。
表2某加氣站計量正確的流量計用氣設備停機前后連續數據記錄
| 溫度/℃ |
壓力/kPa |
瞬時工況流量/(m3·h-1) |
采集時間 |
26.92 |
282.756 |
263.20 |
2016-09-129:16 |
26.63 |
282.261 |
263.19 |
2016-09-129:18 |
26.78 |
282.696 |
263.19 |
2016-09-129:20 |
26.51 |
282.184 |
60.20 |
2016-09-129:22 |
26.50 |
288.762 |
1.90 |
2016-09-129:24 |
26.20 |
288.735 |
0.00 |
2016-09-129:26 |
由表2可以看出,流量計瞬時工況流量從用氣設備運行時的263.19m3/h依次變為運行設備停機后的60.20m3/h、1.90m3/h的小流量(停機延時流量)數據傳回,由于監控系統每2min傳回一條數據,因此,當系統傳回至少一條停機延時流量時,可認為此流量計慣性旋轉時間大于120s,經多次比對判定其運行工況良好,而后經現場拆表檢查,該流量計機芯內部干凈無異物,后送至檢測中心檢定,其低區誤差在誤差允許范圍內。
機械摩擦力矩大的流量計在用氣設備停機后往往沒有小流量運行數據傳輸。某加氣站機械摩擦力矩大的流量計在用氣設備停用時連續數據記錄見表3。
由表3可以看出,當用氣設備停用后,沒有小流量(停機延時流量)數據傳回,而是直接從運行流量438.95m3/h變為0,而后經現場拆表檢查,該流量計機芯的軸與軸承磨損嚴重,后送至檢測中心檢定,其低區誤差不合格。因此判定其機械摩擦力矩Mτm增大,葉輪的旋轉角速度降低,運行工況較差,發生機械慢表的可能性高。
表3某加氣站機械摩擦力矩大的流量計用氣設備停用時連續數據記錄
| 溫度/℃ |
壓力/kPa |
瞬時工況流量/(m3·h-1) |
采集時間 |
22.84 |
258.615 |
438.95 |
2016-09-1210:24 |
22.70 |
258.412 |
438.94 |
2016-09-1210:26 |
22.71 |
258.645 |
438.92 |
2016-09-1210:28 |
22.63 |
258.191 |
438.94 |
2016-09-1210:30 |
22.60 |
262.212 |
438.95 |
2016-09-1210:32 |
22.50 |
262.335 |
0.00 |
2016-09-1210:34 |
4基于停機延時流量的評估方法
4.1渦輪流量計停機延時流量評估模型
根據不同用戶用氣規律的差異性,每個用戶用氣設備每天的停機次數各不相同,要反映流量計實時運行工況,不能只根據一條停機后的數據判斷流量計的準確度,而是需要選取近期的多次停機數據進行評估。
為了確保所統計的停機數據能更加充分、準確地反映流量計實時運行工況,建立流量計停機延時流量評估得分計算式:

式中
S———滿分為100分的情況下,評估周期內流量計停機延時流量評估得分,分
n———評估周期內有停機延時流量傳回的停機次數,次
N———評估周期內該流量計的用氣設備總停機次數,次
式(5)針對某一臺流量計N次停機后的數據進行統計,其中n次有停機延時流量,(N-n)次無停機延時流量。根據以往經驗,當N越大,即計算的總停機次數越多時,評估準確度越高。但是N越大意味著評估周期越長,流量計運行實時工況評估時效性降低,且工作量增大。因此N的取值需要進一步討論。
4.2停機延時流量評估模型的貝葉斯定理實證
①實驗流程
有別于經典統計學派,貝葉斯定理不僅考慮了樣本信息,而且考慮了決策人員所擁有的知識、經驗等私人信息,甚至包含著其主觀判斷。貝葉斯定理綜合樣本信息與先驗信息后進行計算,可能更科學合理,而且可進一步隨著新的實驗信息的增加不斷地進行越來越符合實際的調整與修正。先驗概率是實驗前根據以往積累的資料和經驗,對事件發生可能性的一個預設;后驗概率是在實驗后,根據實驗獲得的信息對事件發生的可能性作重新審視和修正的概率。后驗概率往往對事件發生與否有更為準確的判斷,但需要設計隨機實驗來實現[3]。
貝葉斯定理驗證評估模型的實驗流程見圖2。貝葉斯定理驗證評估模型的實驗流程具體說明如下。
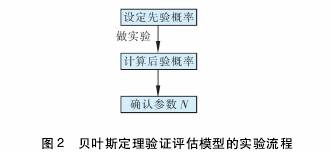
a.對于擬定的參數N,根據以往實踐經驗預設一個先驗概率;
b.做實驗,根據實驗結果用貝葉斯公式計算后驗概率;
c.驗證得出的后驗概率是否達到預定要求,根據結果最終確定參數N。
②N設為20次時的實驗過程
現以LWQZ-100B流量計為例,根據式(5),當某臺LWQZ-100B流量計停機延時流量評估得分S≤20分時,可以判定為機械慢表。此判斷產生2種意見,意見1:此評分發現該型號機械慢表的正確≥a1,a1為此評分發現該型號機械慢表的正確的下限值,取90%;意見2:此評分發現該型號機械慢表的正確≤a2,a2為此評分發現該型號機械慢表的正確的上限值,70%。將意見1記為A1,意見2記為A2。對于這兩種意見工作人員決定用做實驗的方法確定其可信度。實驗方法是根據式(5)計算并統計出x臺機械慢表,然后把這x臺流量計上檢測臺檢測驗證,然后計算可信度。
首先將N設定為20次,即針對某一臺LWQZ-100B流量計統計計算其評估周期內最近的20次的停機數據。根據以往經驗,工作人員認為意見1的可信度為60%,意見2的可信度為40%。記為P(A1)=60%,P(A2)=40%,此概率為先驗概率。
a.第1次實驗。用式(5)針對所監控的逾1000塊規格為LWQZ-100B流量計隨機計算,并選取其中5塊S≤20分的流量計。經檢測臺檢測后發現,該5塊流量計中有3塊確實為機械慢表,2塊不是機械慢表。設B表示事件:x塊流量計中有y塊為機械慢表。
所用到的貝葉斯公式[4]如下:
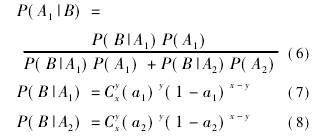
式中
P(A1|B)———B發生的情況下A1的可信度
B———事件:經檢測臺檢測,x塊流量計中有y塊機械慢表
P(B|A1)———A1發生的情況下B的可信度
P(A1)———第1種意見的可信度,其中A1為第1種意見
P(B|A2)———A2發生的情況下B的可信度
P(A2)———第2種意見的可信度,其中A2為第2種意見
x———實驗中,取出的S≤20分的流量計數量,塊
y———實驗中,x塊流量計中確實為機械慢表的流量計數量,塊
a1———意見1中正確的下限值,取90%
a2———正確的上限值,取70%
根據式(6)~(8)可得,B發生的情況下A1的可信度為26.16%,即后驗概率P(A1|B)=26.16%,P(A2|B)=73.84%。該實驗證明A1和A2的先驗概率有問題,需要再做第2次實驗。
b.第2次實驗。用式(5)針對所監控的逾1000塊規格為LWQZ-100B流量計重新隨機計算,并取其中10塊S≤20分的流量計。經檢測臺檢測后發現,該10塊流量計中有7塊確實為機械慢表,3塊不是機械慢表。設C表示事件:10塊流量計中有7塊為機械慢表。
用C事件代替式(6)~(8)中的B事件,計算可得C發生的情況下A1的可信度為7.08%,即后驗概率為P(A1|C)=7.08%,P(A2|C)=92.92%。
實驗1、2說明,當N設定為20次時,發現機械慢表的正確不高于70%的可信度已達92.92%,發現機械慢表的正確較低。
③N設為30次時的實驗過程
現將N調整為30次,即針對某一臺LWQZ-100B流量計統計計算其評估周期內最近的30次的停機數據。根據以往經驗,工作人員認為意見1的可信度為60%,意見2的可信度為40%。即P(A1)=60%,P(A2)=40%,此概率為先驗概率。
a.第1次實驗。用式(5)針對所監控的逾1000塊規格為LWQZ-100B流量計重新隨機計算,并取其中5塊S≤20分的流量計,經檢測臺檢測后發現,該5塊流量計中有5塊確實為機械慢表。設D表示事件:5塊流量計中有5塊為機械慢表。
用D事件代替式(6)~(8)中的B事件,計算可得D發生的情況下A1的可信度為84.06%,即后驗概率為P(A1|D)=84.06%,P(A2|D)=15.94%,這種情形需要再做第2次實驗。
b.第2次實驗。用式(5)針對所監控的逾1000塊規格為LWQZ-100B流量計重新隨機計算,并取其中10塊S≤20分的流量計,經檢測臺檢測后發現,該10塊流量計中有9塊確實為機械慢表。設E表示事件:10塊流量計中有9塊為機械慢表。
用E事件代替式(6)~(8)中的B事件,計算可得E發生的情況下A1的可信度為94.94%,即后驗概率為P(A1|E)=94.94%,P(A2|E)=5.06%。此實驗說明,當N設定為30次,通過式(5)計算型號為LWQZ-100B的流量計最近的30條停機數據,當該流量計停機延時流量評分S≤20分時,此評分發現機械慢表的正確≥90%的可信度已達到94.94%。
當N設定為30次時,此評分模型發現型號為LWQZ-100B的流量計為機械慢表的正確較高。現假設客戶用氣設備每天至少停機1次,則評估周期最多需要30d。
以上為型號為LWQZ-100B流量計的停機延時評分機制,其他型號流量計也可通過此流程建立類似的停機延時評分機制。對先驗概率與后驗概率的比較可以看出,應用貝葉斯定理有利于使工程師的經驗、現場實驗成果以及歷史實驗資料都充分發揮作用,有利于積累資料的同時豐富經驗,是少投入多產出的好方法。
5結論
①將渦輪流量計機械慢表的故障程度隨時量化,大幅度降低不同型號流量計因機械摩擦力矩增加造成機械慢表的發現周期,將故障發現周期從2a縮短到30d,最大程度上降低燃氣公司的經濟損失,從而為企業營收做貢獻。
②對燃氣行業工商大表傳統管理模式創新。通過應用該技術,可以將“首檢合格、定期周檢、到期報廢”的傳統管理模式演變為“首檢合格、隨時評估、永遠如新”的管理模式。
以上內容來源于網絡,如有侵權請聯系即刪除!